Əyri trapesiya G sahəsini necə tapacağımızı anladıq. Budur nəticədə düsturlar:
seqmentdə davamlı və mənfi olmayan y=f(x) funksiyası üçün,
seqmentdə davamlı və qeyri-müsbət funksiya üçün y=f(x).

Bununla belə, ərazinin tapılması ilə bağlı problemləri həll edərkən, çox vaxt daha mürəkkəb rəqəmlərlə məşğul olmaq məcburiyyətindəsiniz.

Bu yazıda sərhədləri funksiyalar tərəfindən açıq şəkildə, yəni y=f(x) və ya x=g(y) kimi göstərilən fiqurların sahəsinin hesablanması haqqında danışacağıq və tipik həllini ətraflı təhlil edəcəyik. misallar.

Səhifə naviqasiyası.

y=f(x) və ya x=g(y) xətləri ilə sərhədlənmiş fiqurun sahəsini hesablamaq üçün düstur.

Teorem.

Qoy və funksiyaları müəyyən edilmiş və intervalda davamlı olsun və hər hansı x dəyəri üçün -dən. Sonra xətlərlə sərhədlənmiş G rəqəminin sahəsi x=a , x=b , və düsturla hesablanır .

Bənzər bir düstur y=c, y=d xətləri ilə məhdudlaşan fiqurun sahəsi üçün etibarlıdır və: .

Sübut.

Düsturun etibarlılığını üç hal üçün göstərək:

Birinci halda, hər iki funksiya qeyri-mənfi olduqda, sahənin əlavə xüsusiyyətinə görə, orijinal G fiqurunun və əyri xətti trapezoidin sahəsinin cəmi rəqəmin sahəsinə bərabərdir. Beləliklə,

Buna görə də, . Son keçid müəyyən inteqralın üçüncü xassəsinə görə mümkündür.

Eynilə, ikinci halda bərabərlik doğrudur. Budur qrafik təsvir:

Üçüncü halda, hər iki funksiya qeyri-müsbət olduqda, bizdə var. Bunu misal gətirək:

İndi funksiyalar və Öküz oxunu kəsdikdə ümumi vəziyyətə keçə bilərik.

Kəsişmə nöqtələrini qeyd edək. Bu nöqtələr seqmenti n hissəyə bölür, burada . G rəqəmi rəqəmlərin birliyi ilə təmsil oluna bilər . Aydındır ki, onun intervalında əvvəllər nəzərdən keçirilən üç haldan birinə düşür, buna görə də onların sahələri kimi tapılır

Beləliklə,

Son keçid müəyyən inteqralın beşinci xassəsinə görə etibarlıdır.

Ümumi işin qrafik təsviri.

Beləliklə, formula sübut edilmişdir.

y=f(x) və x=g(y) xətləri ilə məhdudlaşan fiqurların sahəsini tapmaq nümunələrinin həllinə keçməyin vaxtıdır.

y=f(x) və ya x=g(y) xətləri ilə məhdudlaşan fiqurun sahəsinin hesablanması nümunələri.

Təyyarədə bir fiqur quraraq hər bir problemi həll etməyə başlayacağıq. Bu, bizə mürəkkəb fiquru daha sadə fiqurların birliyi kimi təsəvvür etməyə imkan verəcək. Əgər tikinti ilə bağlı hər hansı bir çətinlik varsa, məqalələrə müraciət edin: ; Və .

Misal.

Parabola ilə məhdudlaşan fiqurun sahəsini hesablayın və düz xətlər, x=1, x=4.

Həll.

Gəlin bu xətləri bir müstəvidə çəkək.

Seqmentin hər yerində parabolanın qrafiki düz xəttin üstündə. Buna görə də, sahə üçün əvvəllər əldə edilmiş düsturları tətbiq edirik və Nyuton-Leybniz düsturundan istifadə edərək müəyyən inteqralı hesablayırıq:

Məsələni bir az mürəkkəbləşdirək.

Misal.

Xətlərlə məhdudlaşan fiqurun sahəsini hesablayın.

Həll.

Bu əvvəlki nümunələrdən nə ilə fərqlənir? Əvvəllər bizdə həmişə x oxuna paralel iki düz xətt vardı, indi isə yalnız bir x=7 var. Dərhal sual yaranır: inteqrasiyanın ikinci həddini haradan əldə etmək olar? Bunun üçün rəsmə nəzər salaq.

Aydın oldu ki, fiqurun sahəsini taparkən inteqrasiyanın aşağı həddi y=x düz xətti ilə yarımparabolanın qrafikinin kəsişmə nöqtəsinin absisidir. Bu absissanı bərabərlikdən tapırıq:

Buna görə də kəsişmə nöqtəsinin absisi x=2-dir.

Qeyd.

Bizim nümunəmizdə və rəsmdə aydın olur ki, xətlər və y=x (2;2) nöqtəsində kəsişir və əvvəlki hesablamalar lazımsız görünür. Ancaq digər hallarda hər şey o qədər də aydın olmaya bilər. Buna görə də, xətlərin kəsişmə nöqtələrinin absis və ordinatlarını həmişə analitik şəkildə hesablamağı tövsiyə edirik.

Aydındır ki, y=x funksiyasının qrafiki interval üzrə funksiyanın qrafikindən yuxarıda yerləşir. Sahəni hesablamaq üçün formula tətbiq edirik:

Tapşırığı daha da çətinləşdirək.

Misal.

Funksiyaların qrafikləri ilə məhdudlaşan fiqurun sahəsini hesablayın və .

Həll.

Gəlin tərs mütənasiblik və parabolaların qrafikini quraq .

Fiqurun sahəsini tapmaq üçün düstur tətbiq etməzdən əvvəl inteqrasiyanın sərhədləri barədə qərar verməliyik. Bunun üçün və ifadələrini bərabərləşdirən xətlərin kəsişmə nöqtələrinin absisini tapacağıq.

X-in sıfırdan fərqli dəyərləri üçün bərabərlik üçüncü dərəcəli tənliyə bərabərdir tam əmsallarla. Onun həlli alqoritmini yadda saxlamaq üçün bölməyə müraciət edə bilərsiniz.

X=1-in bu tənliyin kökü olduğunu yoxlamaq asandır: .

İfadəni bölməklə binomial x-1 üçün bizdə var:

Beləliklə, tənlikdən qalan köklər tapılır :

İndi rəsmdən aydın oldu ki, G rəqəmi intervalda mavinin üstündə və qırmızı xəttin altındadır . Beləliklə, tələb olunan sahə bərabər olacaqdır

Başqa bir tipik nümunəyə baxaq.

Misal.

Əyrilərlə məhdudlaşan fiqurun sahəsini hesablayın və absis oxu.

Həll.

Gəlin rəsm çəkək.

Bu normaldır güc funksiyası eksponent üçdə bir, funksiya qrafiki qrafikdən onu x oxuna nisbətən simmetrik göstərməklə və onu bir yuxarı qaldırmaqla əldə etmək olar.

Bütün xətlərin kəsişmə nöqtələrini tapaq.

Absis oxunun y=0 tənliyi var.

və y=0 funksiyalarının qrafikləri (0;0) nöqtəsində kəsişir, çünki x=0 tənliyin yeganə həqiqi köküdür.

Funksiya qrafikləri və y=0 (2;0) nöqtəsində kəsişir, çünki x=2 tənliyin yeganə köküdür. .

Funksiya qrafikləri və (1;1) nöqtəsində kəsişir, çünki x=1 tənliyin yeganə köküdür . Bu ifadə tamamilə aydın deyil, lakin funksiya ciddi şəkildə artır və - ciddi şəkildə azalan, buna görə də tənlik ən çox bir kökə malikdir.

Yeganə qeyd: bu halda sahəni tapmaq üçün formanın düsturundan istifadə etməli olacaqsınız . Yəni məhdudlaşdırıcı xətlər arqumentin funksiyaları kimi göstərilməlidir y və qara xətt.

Xətlərin kəsişmə nöqtələrini təyin edək.

Funksiyaların qrafiklərindən başlayaq və:

Funksiyaların qrafiklərinin kəsişmə nöqtəsini tapaq və:

Xətlərin kəsişmə nöqtəsini tapmaq qalır və:

Gördüyünüz kimi, dəyərlər eynidir.

Ümumiləşdirin.

Aydın şəkildə müəyyən edilmiş xətlərlə məhdudlaşan bir fiqurun sahəsini tapmaq üçün ən ümumi halları təhlil etdik. Bunu etmək üçün müstəvidə xətlər qurmağı, xətlərin kəsişmə nöqtələrini tapmağı və müəyyən inteqralları hesablamaq qabiliyyətini nəzərdə tutan sahəni tapmaq üçün düsturdan istifadə etməyi bacarmalısınız.

Xətlərlə məhdudlaşan fiqurun sahəsini hesablayın.

Həll.

Verilmiş xətlərin kəsişmə nöqtələrini tapırıq. Bunun üçün tənliklər sistemini həll edirik:

Verilmiş xətlərin kəsişmə nöqtələrinin absislərini tapmaq üçün tənliyi həll edirik:

Biz tapdıq: x 1 = -2, x 2 = 4.

Deməli, parabola və düz xətt olan bu xətlər nöqtələrdə kəsişir A(-2; 0), B(4; 6).

Bu xətlər qapalı bir rəqəm təşkil edir, onun sahəsi yuxarıdakı düsturla hesablanır:

Nyuton-Leybniz düsturundan istifadə edərək tapırıq:

Ellipslə həmsərhəd olan bölgənin sahəsini tapın.

Həll.

Birinci kvadrant üçün ellipsin tənliyindən əldə edirik. Buradan düsturdan istifadə edərək əldə edirik

Gəlin əvəzetmə tətbiq edək x = a günah t, dx = a cos t dt. İnteqrasiyanın yeni hədləri t = α Və t = β 0 = tənliklərindən müəyyən edilir a günah t, a = a günah t. qoymaq olar α = 0 və β = π /2.

Tələb olunan sahənin dörddə birini tapın

Buradan S = πab.

Xətlərlə məhdudlaşan fiqurun sahəsini tapıny = - x 2 + x + 4 vəy = - x + 1.

Həll.

Xətlərin kəsişmə nöqtələrini tapaq y = -x 2 + x + 4, y = -x+ 1, xətlərin ordinatlarını bərabərləşdirir: - x 2 + x + 4 = -x+ 1 və ya x 2 - 2x- 3 = 0. Kökləri tapmaq x 1 = -1, x 2 = 3 və onların müvafiq ordinatları y 1 = 2, y 2 = -2.

Fiqurun sahəsi üçün düsturdan istifadə edərək əldə edirik

Parabola ilə əhatə olunmuş sahəni təyin ediny = x 2 + 1 və düzx + y = 3.

Həll.

Tənliklər sisteminin həlli

kəsişmə nöqtələrinin absisini tapın x 1 = -2 və x 2 = 1.

İnanmaq y 2 = 3 - x Və y 1 = x 2 + 1, aldığımız düstur əsasında

Bernoulli lemniscate daxilində olan ərazini hesablayınr 2 = a 2 cos 2 φ .

Həll.

Qütb koordinat sistemində, əyri qövslə məhdudlaşan fiqurun sahəsi r = f(φ ) və iki qütb radiusu φ 1 = ʅ Və φ 2 = ʆ , inteqral ilə ifadə olunacaq

Əyrinin simmetriyasına görə əvvəlcə tələb olunan sahənin dörddə birini təyin edirik

Beləliklə, bütün sahə bərabərdir S = a 2 .

Astroidin qövs uzunluğunu hesablayınx 2/3 + y 2/3 = a 2/3 .

Həll.

Astroid tənliyini formada yazaq

(x 1/3) 2 + (y 1/3) 2 = (a 1/3) 2 .

qoyaq x 1/3 = a 1/3 cos t, y 1/3 = a 1/3 günah t.

Buradan astroidin parametrik tənliklərini əldə edirik

x = a cos 3 t, y = a günah 3 t, (*)

harada 0 ≤ t ≤ 2π .

Əyrinin (*) simmetriyasına görə qövs uzunluğunun dörddə birini tapmaq kifayətdir. L, parametr dəyişikliyinə uyğundur t 0-dan π /2.

alırıq

dx = -3a cos 2 t günah t dt, dy = 3a günah 2 t cos t dt.

Buradan tapırıq

0-dan alınan ifadənin inteqrasiyası π /2, alırıq

Buradan L = 6a.

Arximed spiralının əhatə etdiyi sahəni tapınr = aφ və qütb bucaqlarına uyğun gələn iki radius vektoruφ 1 Vəφ 2 (φ 1 < φ 2 ).

Həll.

Əyri ilə əhatə olunmuş sahə r = f(φ ) düsturu ilə hesablanır, burada α Və β - qütb bucağının dəyişmə hədləri.

Beləliklə, alırıq

(*)

(*) dən belə nəticə çıxır ki, qütb oxu ilə məhdudlaşan sahə və Arximed spiralinin birinci döngəsi ( φ 1 = 0; φ 2 = 2π ):

Eynilə, qütb oxu və Arximed spiralinin ikinci döngəsi ilə məhdudlaşan sahəni tapırıq ( φ 1 = 2π ; φ 2 = 4π ):

Tələb olunan sahə bu sahələrin fərqinə bərabərdir

Bir ox ətrafında fırlanmaqla əldə edilən cismin həcmini hesablayınöküz parabolalarla məhdudlaşan rəqəmləry = x 2 Vəx = y 2 .

Həll.

Tənliklər sistemini həll edək

və alırıq x 1 = 0, x 2 = 1, y 1 = 0, y 2 = 1, buradan əyrilərin kəsişmə nöqtələri O(0; 0), B(on bir). Şəkildən göründüyü kimi, inqilab gövdəsinin tələb olunan həcmidir fərqə bərabərdir bir ox ətrafında fırlanma nəticəsində əmələ gələn iki həcm öküzəyrixətli trapezoidlər O.C.B.A. Və ODBA:

Bir oxla əhatə olunmuş ərazini hesablayınöküz və sinusoidy = günahx seqmentlər üzrə: a) ; b) .

Həll.

a) Seqmentdə günah funksiyası x işarəni qoruyur və buna görə də düstura görə fərz edir y= günah x, Biz tapdıq

b) Seqmentdə sin funksiyası x işarəsini dəyişir. Məsələni düzgün həll etmək üçün seqmenti ikiyə bölmək və [ π , 2π ], hər birində funksiya öz işarəsini qoruyur.

İşarələr qaydasına görə, seqmentdə [ π , 2π ] sahə mənfi işarəsi ilə götürülür.

Nəticədə tələb olunan sahə bərabərdir

Ellipsin fırlanmasından əldə edilən səthlə məhdudlaşan cismin həcmini təyin edinəsas oxun ətrafındaa .

Həll.

Ellipsin koordinat oxlarına nisbətən simmetrik olduğunu nəzərə alsaq, ox ətrafında fırlanma nəticəsində əmələ gələn həcmi tapmaq kifayətdir. öküz sahə OAB, ellipsin sahəsinin dörddə birinə bərabərdir və nəticəni ikiqat artırın.

Bir inqilab cisminin həcmini ilə işarə edək V x; onda düstur əsasında , burada 0 və a- nöqtələrin absisləri B Və A. Ellipsin tənliyindən tapırıq. Buradan

Beləliklə, tələb olunan həcm bərabərdir. (Elips kiçik ox ətrafında fırlandıqda b, bədənin həcmi bərabərdir)

Parabolalarla məhdudlaşan sahəni tapıny 2 = 2 px Vəx 2 = 2 py .

Həll.

Birincisi, inteqrasiya seqmentini təyin etmək üçün parabolaların kəsişmə nöqtələrinin koordinatlarını tapırıq. Orijinal tənlikləri çevirərək və əldə edirik. Bu dəyərləri bərabərləşdirərək və ya alırıq x 4 - 8səh 3 x = 0.

x 4 - 8səh 3 x = x(x 3 - 8səh 3) = x(x - 2səh)(x 2 + 2px + 4səh 2) = 0.

Tənliklərin köklərinin tapılması:

Nəzərə alsaq ki, nöqtə A parabolaların kəsişməsi birinci rübdə, sonra inteqrasiyanın sərhədləridir x= 0 və x = 2səh.

Düsturdan istifadə edərək tələb olunan sahəni tapırıq

Bu dərsdə hesablamağı öyrənəcəyik təyyarə fiqurlarının sahələri adlanır əyrixətli trapezoidlər .

Belə rəqəmlərin nümunələri aşağıdakı şəkildədir.

Bir tərəfdən ərazini tapın düz fiqur müəyyən inteqraldan istifadə olduqca sadədir. Söhbət yuxarıdan müəyyən bir əyri ilə, aşağıdan absis oxu ilə məhdudlaşan fiqurun sahəsindən gedir ( öküz), solda və sağda bəzi düz xətlər var. Sadəlik ondadır əyrinin verildiyi funksiyanın müəyyən inteqralı belə bir rəqəmin sahəsidir(əyrixətli trapesiya).

Fiqurun sahəsini hesablamaq üçün bizə lazımdır:

1. Əyri təyin edən funksiyanın müəyyən inteqralı , yuxarıdan əyri trapesiyanı məhdudlaşdırır. Və burada ilk əhəmiyyətli nüans ortaya çıxır: əyri trapesiya yalnız yuxarıdan deyil, aşağıdan da əyri ilə məhdudlaşdırıla bilər . Bu halda necə davam etmək olar? Sadə, lakin yadda saxlamaq vacibdir: bu halda inteqral mənfi işarəsi ilə alınır .
2. İnteqrasiya məhdudiyyətləri a Və b, onu sol və sağdakı rəqəmi bağlayan xətlərin tənliklərindən tapırıq: x = a , x = b, Harada a Və b- nömrələri.

Ayrı-ayrılıqda, daha bir neçə nüans haqqında.

Əyri trapesiyanı yuxarıdan (və ya aşağıdan) bağlayan əyri olmalıdır davamlı və mənfi olmayan funksiyanın qrafiki y = f(x) .

"x" dəyərləri seqmentə aid olmalıdır [a, b]. Yəni, göbələyin kəsilməsi kimi xətlər nəzərə alınmır, gövdəsi bu seqmentə yaxşı uyğun gəlir və qapaq daha genişdir.

Yan seqmentlər nöqtələrə çevrilə bilər . Rəsmdə belə bir rəqəm görsəniz, bu sizi çaşdırmamalıdır, çünki bu nöqtə həmişə "x" oxunda öz dəyərinə malikdir. Bu o deməkdir ki, inteqrasiya sərhədləri ilə hər şey öz qaydasındadır.

İndi düsturlara və hesablamalara keçə bilərsiniz. Belə ki, ərazi səyri trapesiya düsturundan istifadə etməklə hesablana bilər

Əgər f(x) ≤ 0 (funksiyanın qrafiki oxun altında yerləşir öküz), Yəni əyri trapezoidin sahəsi düsturdan istifadə etməklə hesablana bilər

Fiqurun həm yuxarı, həm də aşağı sərhədlərinin müvafiq olaraq funksiya olduğu hallar da var y = f(x) Və y = φ (x) , onda belə bir rəqəmin sahəsi düsturla hesablanır

. (3)

Problemləri birlikdə həll etmək

Fiqurun sahəsinin (1) düsturu ilə hesablana biləcəyi hallardan başlayaq.

Misal 1.öküz) və düz x = 1 , x = 3 .

Həll. Çünki y = 1/x seqmentdə > 0 olarsa, əyri xətti trapezoidin sahəsi (1) düsturu ilə tapılır:

.

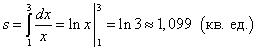Misal 2. Funksiya qrafiki, xətti ilə məhdudlaşan fiqurun sahəsini tapın x= 1 və x oxu ( öküz ).

Həll. Formula (1) tətbiqinin nəticəsi:

Əgər onda s= 1/2; əgər onda s= 1/3 və s.

Misal 3. Funksiya qrafiki, absis oxu ilə məhdudlaşan fiqurun sahəsini tapın ( öküz) və düz x = 4 .

Həll. Məsələnin şərtlərinə uyğun gələn rəqəm sol seqmentin bir nöqtəyə çevrildiyi əyrixətli trapesiyadır. İnteqrasiya hədləri 0 və 4-dür. Çünki (1) düsturundan istifadə edərək əyrixətti trapezoidin sahəsini tapırıq:

.

Misal 4., xətləri ilə sərhədlənmiş və 1-ci rübdə yerləşən fiqurun sahəsini tapın.

Həll. Düsturdan (1) istifadə etmək üçün nümunənin şərtləri ilə verilən fiqurun sahəsini üçbucağın sahələrinin cəmi kimi təsəvvür edək. OAB və əyri trapesiya ABC. Üçbucağın sahəsini hesablayarkən OAB inteqrasiya hədləri nöqtələrin absisləridir O Və A, və rəqəm üçün ABC- nöqtələrin absisləri A Və C (A xəttin kəsişmə nöqtəsidir O.A. və parabolalar, və C- parabolanın oxla kəsişmə nöqtəsi öküz). Düz xəttin və parabolanın tənliklərini birgə (sistem kimi) həll edərək (nöqtənin absisini) alırıq. A) və (həlli üçün lazım olmayan xəttin və parabolanın başqa kəsişmə nöqtəsinin absisi). Eynilə , (nöqtələrin absislərini) əldə edirik C Və D). İndi fiqurun sahəsini tapmaq üçün bizə lazım olan hər şey var. Biz tapdıq:

Misal 5.Əyri trapezoidin sahəsini tapın ACDB, əgər əyrinin tənliyi CD və absislər A Və B müvafiq olaraq 1 və 2.

Həll. Əyrinin bu tənliyini oyun vasitəsilə ifadə edək: Əyrixətti trapezoidin sahəsi (1) düsturu ilə tapılır:

.

Fiqurun sahəsinin (2) düsturundan istifadə edərək hesablana biləcəyi hallara keçək.

Misal 6. Parabola və x oxu ilə məhdudlaşan fiqurun sahəsini tapın ( öküz ).

Həll. Bu rəqəm x oxunun altında yerləşir. Buna görə də onun sahəsini hesablamaq üçün (2) düsturundan istifadə edəcəyik. İnteqrasiya hədləri absislər və parabolanın ox ilə kəsişmə nöqtələridir. öküz. Beləliklə,

Misal 7. Absis oxu arasında qapalı olan sahəni tapın ( öküz) və iki bitişik sinus dalğası.

Həll. Bu rəqəmin sahəsi (2) düsturu ilə tapıla bilər:

.

Hər bir termini ayrıca tapaq:

.

.

Nəhayət ərazini tapırıq:

.

Misal 8. Parabola ilə əyri arasında qalan fiqurun sahəsini tapın.

Həll. Oyun vasitəsilə xətlərin tənliklərini ifadə edək:

Formula (2) uyğun olaraq sahə kimi alınır

,

Harada a Və b- nöqtələrin absisləri A Və B. Tənlikləri birlikdə həll edərək onları tapaq:

Nəhayət ərazini tapırıq:

Və nəhayət, rəqəmin sahəsinin (3) düsturundan istifadə edərək hesablanması halları.

Misal 9. Parabolalar arasında qalan fiqurun sahəsini tapın Və .

Gəlin inteqral hesablamanın tətbiqlərini nəzərdən keçirək. Bu dərsdə tipik və ən ümumi tapşırığı təhlil edəcəyik müəyyən inteqraldan istifadə edərək müstəvi fiqurun sahəsinin hesablanması. Nəhayət, ali riyaziyyatda məna axtaranların hamısı onu tapsın. Heç vaxt bilmirsən. Real həyatda, elementar funksiyalardan istifadə edərək bir bağ sahəsini təxmin etməli və müəyyən bir inteqraldan istifadə edərək sahəsini tapmalı olacaqsınız.

Materialı uğurla mənimsəmək üçün sizə lazımdır:

1) Anlamaq qeyri-müəyyən inteqral heç olmasa orta səviyyədə. Buna görə də, ilk növbədə dummies dərsi oxumalıdır yox.

2) Nyuton-Leybnits düsturunu tətbiq etməyi və müəyyən inteqralı hesablamağı bacarın. Səhifədə müəyyən inteqrallarla isti dostluq münasibətləri qura bilərsiniz Müəyyən inteqral. Həll nümunələri. “Müəyyən bir inteqraldan istifadə edərək sahəni hesablayın” tapşırığı həmişə rəsm çəkməyi əhatə edir, beləliklə, sizin bilik və rəsm bacarıqlarınız da aktual məsələ olacaq. Ən azı düz xətt, parabola və hiperbola qurmağı bacarmalısınız.

Əyri trapesiya ilə başlayaq. Əyri trapesiya hansısa funksiyanın qrafiki ilə məhdudlaşan düz fiqurdur y = f(x), ox ÖKÜZ və xətlər x = a; x = b.

Əyrixətti trapezoidin sahəsi ədədi olaraq müəyyən bir inteqrala bərabərdir

Hər hansı müəyyən inteqralın (mövcud olan) çox yaxşı həndəsi mənası var. Dərsdə Müəyyən inteqral. Həll nümunələri dedik ki, müəyyən inteqral ədəddir. İndi başqa bir faydalı faktı qeyd etməyin vaxtı gəldi. Həndəsə nöqteyi-nəzərindən müəyyən inteqral AREA-dır. Yəni, müəyyən inteqral (əgər varsa) həndəsi olaraq müəyyən bir fiqurun sahəsinə uyğundur. Müəyyən inteqralı nəzərdən keçirək

İnteqral

müstəvidə bir əyri təyin edir (istəsəniz çəkilə bilər) və müəyyən inteqralın özü ədədi olaraq müvafiq əyrixətti trapezoidin sahəsinə bərabərdir.

Misal 1

, , , .

Bu tipik bir tapşırıq bəyanatıdır. Qərarda ən vacib məqam rəsmin qurulmasıdır. Üstəlik, rəsm qurulmalıdır SAĞ.

Bir rəsm qurarkən aşağıdakı ardıcıllığı tövsiyə edirəm: əvvəlcə bütün düz xətləri (əgər onlar varsa) qurmaq daha yaxşıdır və yalnız Sonra– parabola, hiperbola, digər funksiyaların qrafikləri. Nöqtə-nöqtə tikinti texnikası istinad materialında tapıla bilər Qrafiklər və xassələr elementar funksiyalar . Orada dərsimiz üçün çox faydalı material tapa bilərsiniz - parabolanı necə tez qurmaq olar.

Bu problemdə həll yolu belə görünə bilər.

Gəlin rəsm çəkək (tənliyi qeyd edin y= 0 oxu təyin edir ÖKÜZ):

Əyri trapesiyaya kölgə salmayacağıq, burada hansı sahədən bəhs etdiyimiz aydındır. Həll belə davam edir:

Seqmentdə [-2; 1] funksiya qrafiki y = x 2+2 yerləşir oxun üstündəÖKÜZ, Buna görə də:

Cavab: .

Müəyyən inteqralı hesablamaqda və Nyuton-Leybniz düsturunu tətbiq etməkdə çətinlik çəkən

,

mühazirəsinə müraciət edin Müəyyən inteqral. Həll nümunələri. Tapşırığı yerinə yetirdikdən sonra rəsmə baxmaq və cavabın real olub olmadığını anlamaq həmişə faydalıdır. Bu vəziyyətdə, rəsmdəki hüceyrələrin sayını "gözlə" hesablayırıq - yaxşı, təxminən 9 olacaq, bu doğru görünür. Tamamilə aydındır ki, deyək ki, cavabı alsaq: 20 kvadrat vahid, onda haradasa səhv edildiyi açıqdır - 20 hüceyrə açıq-aydın sözügedən rəqəmə uyğun gəlmir, ən çoxu onlarla. Cavab mənfi olarsa, tapşırıq da səhv həll edilmişdir.

Misal 2

Xətlərlə məhdudlaşan fiqurun sahəsini hesablayın xy = 4, x = 2, x= 4 və ox ÖKÜZ.

Bu bir nümunədir müstəqil qərar. Tam həll və dərsin sonunda cavab.

Əyri trapezoid yerləşirsə nə etməli oxun altındaÖKÜZ?

Misal 3

Xətlərlə məhdudlaşan fiqurun sahəsini hesablayın y = e-x, x= 1 və koordinat oxları.

Həlli: Gəlin rəsm çəkək:

Əgər əyri trapesiya tamamilə oxun altında yerləşir ÖKÜZ , onda onun sahəsi düsturla tapıla bilər:

Bu halda:

.

Diqqət! İki növ tapşırıq qarışdırılmamalıdır:

1) Əgər sizdən sadəcə olaraq müəyyən bir inteqralı heç biri olmadan həll etməyiniz xahiş olunursa həndəsi məna, onda mənfi ola bilər.

2) Əgər sizdən müəyyən inteqraldan istifadə edərək fiqurun sahəsini tapmaq istənilirsə, onda sahə həmişə müsbətdir! Ona görə də indicə müzakirə olunan düsturda mənfi görünür.

Praktikada çox vaxt rəqəm həm yuxarı, həm də aşağı yarım müstəvidə yerləşir və buna görə də ən sadə məktəb problemlərindən daha mənalı nümunələrə keçirik.

Misal 4

Xətlərlə məhdudlaşan təyyarə fiqurunun sahəsini tapın y = 2x – x 2 , y = -x.

Həll yolu: Əvvəlcə bir rəsm çəkməlisiniz. Sahə problemlərində rəsm qurarkən bizi ən çox xətlərin kəsişmə nöqtələri maraqlandırır. Parabolanın kəsişmə nöqtələrini tapaq y = 2x – x 2 və düz y = -x. Bu iki yolla edilə bilər. Birinci üsul analitikdir. Tənliyi həll edirik:

Bu, inteqrasiyanın aşağı sərhədi deməkdir a= 0, inteqrasiyanın yuxarı həddi b= 3. Çox vaxt xətləri nöqtə-nöqtə qurmaq daha sərfəli və daha sürətli olur və inteqrasiyanın sərhədləri “özlüyündə” aydın olur. Buna baxmayaraq, məsələn, qrafik kifayət qədər böyükdürsə və ya təfərrüatlı konstruksiya inteqrasiyanın hüdudlarını aşkar etmirsə (onlar fraksiya və ya irrasional ola bilər) həddi tapmaq üçün analitik metoddan hələ də bəzən istifadə edilməlidir. Gəlin vəzifəmizə qayıdaq: əvvəlcə düz xətt, sonra isə parabola qurmaq daha rasionaldır. Gəlin rəsm çəkək:

Təkrar edək ki, nöqtəvi qurarkən inteqrasiyanın hədləri ən çox "avtomatik" olaraq müəyyən edilir.

İndi iş düsturu:

Əgər seqmentdə [ a; b] bəzi davamlı funksiya f(x) -dən böyük və ya bərabərdir bəzi davamlı funksiya g(x), onda müvafiq rəqəmin sahəsi düsturla tapıla bilər:

Burada artıq rəqəmin harada yerləşdiyini düşünmək lazım deyil - oxun üstündə və ya oxun altında, ancaq hansı qrafikin DAHA YÜKSƏK olması vacibdir(başqa bir qrafikə nisbətən), və hansı AŞAĞIDA.

Baxılan misalda seqmentdə parabolanın düz xəttin üstündə yerləşdiyi və buna görə də 2-dən aydın görünür. x – x 2 çıxılmalıdır - x.

Tamamlanmış həll bu kimi görünə bilər:

İstədiyiniz rəqəm parabola ilə məhdudlaşır y = 2x – x 2 üst və düz y = -x aşağıda.

2-ci seqmentdə x – x 2 ≥ -x. Müvafiq düstura görə:

Cavab: .

Əslində, aşağı yarım müstəvidə əyri bir trapezoidin sahəsi üçün məktəb düsturu (3 nömrəli nümunəyə baxın) formulun xüsusi bir vəziyyətidir.

.

Çünki ox ÖKÜZ tənliyi ilə verilir y= 0 və funksiyanın qrafiki g(x) oxun altında yerləşir ÖKÜZ, Bu

.

İndi öz həlliniz üçün bir neçə nümunə

Misal 5

Misal 6

Xətlərlə məhdudlaşan fiqurun sahəsini tapın

Müəyyən bir inteqraldan istifadə edərək sahənin hesablanması ilə bağlı məsələləri həll edərkən bəzən gülməli bir hadisə baş verir. Rəsm düzgün çəkilib, hesablamalar düzgün aparılıb, lakin diqqətsizlikdən... Səhv fiqurun sahəsi tapıldı.

Misal 7

Əvvəlcə bir rəsm çəkək:

Sahəsini tapmalı olduğumuz rəqəm mavi rəngdədir(şərtə diqqətlə baxın - rəqəm necə məhduddur!). Ancaq praktikada, diqqətsizlik səbəbindən, çox vaxt fiqurun kölgəli sahəsini tapmaq lazım olduğuna qərar verirlər. yaşıl!

Bu nümunə həm də faydalıdır, çünki iki müəyyən inteqraldan istifadə edərək rəqəmin sahəsini hesablayır. Həqiqətən:

1) Seqmentdə [-1; 1] oxun üstündə ÖKÜZ qrafik düz yerləşir y = x+1;

2) Oxun üstündəki seqmentdə ÖKÜZ hiperbolanın qrafiki yerləşir y = (2/x).

Sahələrin əlavə oluna biləcəyi (və edilməlidir), buna görə də aydındır:

Cavab:

Misal 8

Xətlərlə məhdudlaşan fiqurun sahəsini hesablayın

Tənlikləri “məktəb” şəklində təqdim edək

və nöqtəli bir rəsm çəkin:

Rəsmdən aydın olur ki, yuxarı limitimiz "yaxşıdır": b = 1.

Amma aşağı hədd nədir?! Aydındır ki, bu tam deyil, amma nədir?

Ola bilər, a=(-1/3)? Ancaq rəsmin mükəmməl dəqiqliklə edildiyinə zəmanət haradadır, yaxşı olar ki a=(-1/4). Qrafiki səhv qursaq nə olacaq?

Belə hallarda əlavə vaxt sərf etməli və analitik şəkildə inteqrasiyanın sərhədlərini aydınlaşdırmalısınız.

Qrafiklərin kəsişmə nöqtələrini tapaq

Bunu etmək üçün tənliyi həll edirik:

.

Beləliklə, a=(-1/3).

Əlavə həll yolu mənasızdır. Əsas odur ki, əvəzləmələrdə və işarələrdə çaşqınlıq olmasın. Buradakı hesablamalar ən sadə deyil. Seqmentdə

, ,

müvafiq düstura görə:

Cavab:

Dərsi yekunlaşdırmaq üçün daha iki çətin işə baxaq.

Misal 9

Xətlərlə məhdudlaşan fiqurun sahəsini hesablayın

Həlli: Gəlin rəsmdə bu rəqəmi təsvir edək.

Nöqtə-nöqtəli bir rəsm qurmaq üçün sinusoidin görünüşünü bilmək lazımdır. Ümumiyyətlə, bütün elementar funksiyaların qrafiklərini, eləcə də bəzi sinus qiymətlərini bilmək faydalıdır. Onlar dəyərlər cədvəlində tapıla bilər triqonometrik funksiyalar . Bəzi hallarda (məsələn, bu halda) qrafiklər və inteqrasiya hədləri əsaslı şəkildə düzgün göstərilməli olan sxematik bir rəsm qurmaq mümkündür.

Burada inteqrasiyanın sərhədləri ilə bağlı heç bir problem yoxdur, onlar birbaşa şərtdən irəli gəlir:

– “x” sıfırdan “pi”yə dəyişir. Gəlin əlavə qərar verək:

Seqmentdə, funksiyanın qrafiki y= günah 3 x oxun üstündə yerləşir ÖKÜZ, Buna görə də:

(1) Sinusların və kosinusların tək güclərdə necə inteqrasiya olunduğunu dərsdə görə bilərsiniz Triqonometrik funksiyaların inteqralları. Bir sinusu sıxırıq.

(2) Biz formada əsas triqonometrik eynilikdən istifadə edirik

(3) Gəlin dəyişəni dəyişdirək t= cos x, onda: oxun üstündə yerləşir, buna görə də:

.

.

Qeyd: kubdakı tangensin inteqralının necə alındığına diqqət yetirin; burada əsas olanın nəticəsi istifadə olunur. triqonometrik eynilik

.

İnteqralı tapmaq üçün lazım olan funksiyanı daxil edin

Kalkulyator təmin edir ƏTRAFLI HƏLL müəyyən inteqrallar.

Bu kalkulyator f(x) funksiyasının müəyyən inteqralının yuxarı və aşağı hədləri verilmiş həllini tapır.

Nümunələr

Dərəcədən istifadə
(kvadrat və kub) və kəsrlər

(x^2 - 1)/(x^3 + 1)

Kvadrat kök

Sqrt(x)/(x + 1)

Kub kökü

Cbrt(x)/(3*x + 2)

Sinus və kosinusdan istifadə

2*sin(x)*cos(x)

arcsine

X*arcsin(x)

qövs kosinusu

X*arccos(x)

Loqarifmin tətbiqi

X*log(x, 10)

Təbii loqarifm

Sərgi iştirakçısı

Tg(x)*sin(x)

Kotangent

Ctg(x)*cos(x)

İrrasional kəsrlər

(sqrt(x) - 1)/sqrt(x^2 - x - 1)

Arktangent

X*arctg(x)

Arkkotangent

X*arсctg(x)

Hiperbolik sinus və kosinus

2*sh(x)*ch(x)

Hiperbolik tangens və kotangens

Ctgh(x)/tgh(x)

Hiperbolik arksin və arkkosin

X^2*arcsinh(x)*arccosh(x)

Hiberbolik arktangent və arkotangens

X^2*arctgh(x)*arcctgh(x)

İfadələrin və funksiyaların daxil edilməsi qaydaları

İfadələr funksiyalardan ibarət ola bilər (qeydiyyatlar əlifba sırası ilə verilir): mütləq(x) Mütləq dəyər x
(modul x və ya |x|) arccos(x) Funksiya - qövs kosinusu x arkkoş(x) Qövs kosinusu hiperbolik x arcsin(x) Arcsine from x arcsinh(x) Arcsine hiperbolik x arktan(x) Funksiya - arktangens x arctgh(x) Arktangens hiperbolik x e e təxminən 2.7-yə bərabər olan bir rəqəm exp(x) Funksiya - göstəricisi x(kimi e^x) log(x) və ya ln(x) Təbii loqarifmi x
(Almaq üçün log7(x), log(x)/log(7) daxil etməlisiniz (və ya, məsələn, üçün log10(x)=log(x)/log(10)) pi Bu rəqəm təxminən 3,14-ə bərabər olan "Pi"dir günah(x) Funksiya - Sinus x cos(x) Funksiya - kosinus x sinh(x) Funksiya - Sinus hiperbolik x cosh(x) Funksiya - Kosinus hiperbolik x sqrt(x) Funksiya - Kvadrat kök-dan x sqr(x) və ya x^2 Funksiya - Kvadrat x tan(x) Funksiya - dən tangens x tgh(x) Funksiya - tangent hiperbolik x cbrt(x) Funksiya - kub kökü-dan x

İfadələrdə aşağıdakı əməliyyatlardan istifadə edilə bilər: Həqiqi rəqəmlər kimi daxil edin 7.5 , Yox 7,5 2*x- vurma 3/x- bölmə x^3- eksponentasiya x+7- əlavə x - 6- çıxma
Digər xüsusiyyətlər: mərtəbə(x) Funksiya - yuvarlaqlaşdırma x aşağı (məsələn mərtəbə(4.5)==4.0) tavan(x) Funksiya - yuvarlaqlaşdırma x yuxarı (misal tavan(4.5)==5.0) işarəsi(x) Funksiya - İşarə x erf(x) Səhv funksiyası (və ya ehtimal inteqralı) laplace(x) Laplas funksiyası