Fiqurun sahəsinin hesablanması.

Seçmə üsulu

İrkutskdakı 23 nömrəli MBOU orta məktəbin 5B sinif şagirdinin işi

Balsukova Alexandra

Rəhbər: Khodyreva T.G.

2014

Fiqurun sahəsinin hesablanması. Seçmə üsulu

Tədqiqat obyekti : damalı kağız üzərində tapşırıqlar

Tədqiqat mövzusu : damalı kağızda çoxbucaqlının sahəsinin hesablanması problemləri, onların həlli üsulları və üsulları.

Tədqiqat üsulları Açar sözlər: müqayisə, ümumiləşdirmə, analogiya, ədəbiyyat və internet resurslarının öyrənilməsi, informasiya təhlili.

Tədqiqatın məqsədi:

əsas, maraqlı, başa düşülən məlumatları seçin

Alınan məlumatları təhlil edin və təşkil edin

Damalı kağızda məsələlərin həlli üçün müxtəlif üsul və üsulları tapın

Pik düsturundan istifadə edərək həndəsi fiqurların sahələrini hesablamaq üçün düsturları yoxlayın

Toplanmış materialı təqdim etmək üçün işin elektron təqdimatını yaradın

Həndəsə zehni qabiliyyətlərimizi təkmilləşdirmək üçün ən güclü vasitədir və düzgün düşünməyə və düşünməyə imkan verir.

(G. Galileo)

Mövzunun aktuallığı

Riyaziyyata həvəs çox vaxt problem haqqında düşünməklə başlayır. Beləliklə, “Çoxbucaqlıların sahələri” mövzusunu öyrənərkən sual yaranır ki, dərslikdə nəzərdə tutulan tapşırıqlardan fərqli tapşırıqlar varmı? Belə tapşırıqlara damalı kağız üzərində tapşırıqlar daxildir. Belə məsələlərin özəlliyi nədir, damalı kağızda məsələlərin həlli üçün xüsusi üsul və üsullar varmı? Riyaziyyat dərsində müəllim bizi çoxbucaqlıların hesablanması üçün maraqlı üsulla tanış etdi. Bu mövzuda ədəbiyyatı, internet resurslarını öyrənməyə başladım. Görünür ki, füsunkar şeyləri damalı müstəvidə, yəni eyni kvadratlara düzülmüş sonsuz bir kağız parçasında tapmaq olar. Məlum olub ki, damalı kağızla bağlı tapşırıqlar kifayət qədər müxtəlifdir. Damalı kağız üzərində çəkilmiş çoxbucaqlıların sahələrini hesablamağı öyrəndim. Bir çox tapşırıqlar üçün damalı kağız yoxdur ümumi qayda həllər, xüsusi metodlar və texnikalar. Bu, onların xüsusi bir təhsil bacarığının və ya bacarığının deyil, ümumiyyətlə düşünmək, əks etdirmək, təhlil etmək, analogiyalar axtarmaq qabiliyyətinin inkişafı üçün dəyərini müəyyən edən xüsusiyyətidir, yəni bu tapşırıqlar geniş mənada düşünmə bacarıqlarını inkişaf etdirir.

Və mən də öyrəndim ki, bu cür tapşırıqlar DİA və Vahid Dövlət İmtahanının nəzarət-ölçü materiallarında nəzərdən keçirilir. Buna görə də bu materialın öyrənilməsini təkcə gələcəkdə deyil, tətbiqi üçün faydalı hesab edirəm təhsil prosesi, həm də qeyri-standart olimpiada məsələlərini həll etmək üçün.

2.Ərazi anlayışı

Kvadrat- ikiölçülün ədədi xarakteristikası həndəsi fiqur, bu formanın ölçüsünü göstərir. Tarixən ərazinin hesablanması adlanırdı . Sahəsi olan fiqur deyilir kvadratlaşdırma .

Həndəsə baxımından düz bir fiqurun sahəsi

1. Kvadrat- kənarı bir uzunluğa bərabər olan kvadrat olan standart fiqurla münasibətdə düz fiqurun ölçüsü.

2. Kvadrat- müəyyən bir sinfin yastı fiqurlarına (məsələn, çoxbucaqlılara) aid edilən ədədi xarakteristikası. Bir tərəfi uzunluq vahidinə bərabər olan kvadratın sahəsi, sahə vahidinə bərabər götürülür

3. Kvadrat- ədədi dəyəri aşağıdakı xüsusiyyətlərə malik olan müsbət qiymət:

 Bərabər rəqəmlər bərabər sahələrə malikdir;

 Əgər rəqəm sadə fiqurlar olan hissələrə bölünürsə (yəni sonlu sayda düz üçbucaqlara bölünə bilənlər), onda bu rəqəmin sahəsi onun sahələrinin cəminə bərabərdir. hissələri;

 Ölçü vahidinə bərabər bir tərəfi olan kvadratın sahəsi birə bərabərdir.

Beləliklə, belə bir nəticəyə gələ bilərik ki, ərazi xüsusi bir dəyər deyil, ancaq düz bir fiqurun bəzi şərti xarakteristikasını verir. İxtiyari bir fiqurun sahəsini tapmaq üçün tərəfi uzunluq vahidinə bərabər olan neçə kvadratdan ibarət olduğunu müəyyən etmək lazımdır. Məsələn, kvadrat santimetrin tam 6 dəfə uyğun olduğu bir düzbucaqlı götürək. Bu o deməkdir ki, düzbucaqlının sahəsi 6 sm2-dir.

Yan tərəfi ölçü vahidinə bərabər olan kvadratın sahəsinin bütün sahələr üçün minimum ölçü vahidi kimi seçilməsi təsadüfi deyil. Bu, çoxəsrlik "təbii" seçim zamanı insanlar arasında yaranan razılaşmanın nəticəsidir. Bundan əlavə, ölçü vahidi ilə bağlı başqa təkliflər də var idi. Beləliklə, məsələn, bərabərtərəfli üçbucağın sahəsini belə bir vahid kimi götürmək təklif edildi (yəni, hər hansı bir düz rəqəm müəyyən bir ədədin "cəmi" kimi təqdim edilə bilər. bərabərtərəfli üçbucaqlar), ərazilərin ədədi təmsilinin dəyişməsinə səbəb olacaq.

Beləliklə, sahələri hesablamaq üçün düsturlar riyaziyyatda ortaya çıxdı və dərhal bir insan tərəfindən həyata keçirilmədi - bu müxtəlif dövrlərdə və müxtəlif ölkələrdə yaşayan bir çox alimlər. (Yanlış düsturlar elmdə özünə yer tapmadı və unudulub getdi). Əsl düsturlar müasir formada bizə çatana qədər minlərlə il ərzində əlavə edilmiş, düzəldilmiş və əsaslandırılmışdır.

Əlbəttə ərazinin ölçülməsi verilən fiqurun sahəsini ölçü vahidi kimi götürülmüş fiqurun sahəsi ilə müqayisə etməkdən ibarətdir. Müqayisə nəticəsində müəyyən bir rəqəm əldə edilir - verilmiş rəqəmin sahəsinin ədədi dəyəri. Bu rəqəm, verilmiş bir fiqurun sahəsinin sahə vahidi kimi götürülmüş fiqurun sahəsindən neçə dəfə böyük (və ya daha az) olduğunu göstərir.

T Beləliklə, belə bir nəticəyə gələ bilərik ki, ərazi yastı fiqurun bəzi xüsusiyyətlərini ölçmək üçün tarixən insan tərəfindən təqdim edilmiş süni bir kəmiyyətdir. Belə bir dəyərin daxil edilməsi zərurəti bu və ya digər ərazinin nə qədər böyük olduğunu, tarla əkmək və ya bəzək plitələrini bəzəmək üçün döşəmə səthinin sahəsini hesablamaq üçün nə qədər taxıl lazım olduğunu bilmək ehtiyacının artması ilə əlaqədar idi.

Pik Formula

Damalı kağızda çoxbucaqlının sahəsini qiymətləndirmək üçün bu poliqonun neçə hüceyrəni əhatə etdiyini hesablamaq kifayətdir (hüceyrənin sahəsini vahid kimi götürürük). Daha doğrusu, əgərS çoxbucaqlının sahəsi, B tamamilə çoxbucaqlı daxilində yerləşən hüceyrələrin sayı, G isə daxili olan hüceyrələrin sayıdır. Biz yalnız belə çoxbucaqlıları nəzərdən keçirəcəyik, onların bütün təpələri damalı kağızın qovşaqlarında yerləşir - çoxbucaqlının şəbəkə xətlərinin ən azı bir ümumi nöqtənin kəsişdiyi yerlərdə.

Damalı kağıza çəkilmiş hər hansı üçbucağın sahəsi onu düzbucaqlı üçbucaqların və tərəfləri çəkilmiş üçbucağın təpələrindən keçən tor xətlərini izləyən düzbucaqlıların sahələrinin cəmi və ya fərqi kimi təqdim etməklə asanlıqla hesablana bilər.

Belə bir çoxbucağın sahəsini hesablamaq üçün aşağıdakı teoremdən istifadə edə bilərsiniz:

Teorem . Qoy - çoxbucaqlı daxilində tam nöqtələrin sayı, - onun sərhədindəki tam nöqtələrin sayı, - onun sahəsi. SonraPik düsturu:

Misal. Şəkildəki çoxbucaqlı üçünL = 7 (qırmızı nöqtələr), 9 (yaşıl nöqtələr), beləS = 7+ 9/2 -1 = 10,5 kvadrat vahidlər.

Pik teoremi- klassik nəticə və .

Düyünlərində təpələri olan və içərisində və ya tərəflərində heç bir qovşaq olmayan (təpələrdən başqa) üçbucağın sahəsi 1/2-ə bərabərdir. Bu fakt.

3. Tarix

Pik düsturu Avstriyalı riyaziyyatçı Georg Alexander (1859-1942) tərəfindən kəşf edilmişdir. . 16 yaşında Georg məktəbi bitirdi və daxil oldu. 20 yaşında fizika və riyaziyyatdan dərs demək hüququ qazandı. 1884-cü ildə Peak getdiüçün . Orada Kleinin başqa bir tələbəsi ilə tanış oldu.. Daha sonra, 1885-ci ildə o, qayıtdıelmi karyerasının qalan hissəsini burada keçirdi.

Georg Pik Eynşteynlə dost idi. Pik və Eynşteyn təkcə elmi maraqları bölüşmürdülər, həm də musiqiyə həvəsli idilər. Universitet professorlarından ibarət kvartetdə çıxış edən Pik Eynşteyni Praqanın elmi və musiqi cəmiyyətləri ilə tanış etdi.

Pikin riyazi maraq dairəsi son dərəcə geniş idi. Xüsusilə, onların sayı 50-dən çoxdur elmi əsərlər. Onun 1899-cu ildə kəşf etdiyi Pik teoremi çoxbucaqlının sahəsini hesablamaq üçün geniş yayılmışdı. Almaniyada bu teorem məktəb dərsliklərinə daxil edilmişdir.

4.Pik düsturunun tətbiqi

Pick düsturu təkcə çoxbucaqlıların sahələrini hesablamaq üçün deyil, həm də olimpiada səviyyəsinin bir çox məsələlərini həll etmək üçün istifadə olunur.

Problemləri həll edərkən Pik düsturundan istifadə etmək üçün bəzi nümunələr:

1) Şahmat kralı hər birini ziyarət edərək 8 × 8 hücrədən ibarət lövhənin ətrafında gəzdi

ev sahəsi tam bir dəfə və son hərəkətlə orijinala qayıdır

sahə. Sahələrin mərkəzlərini ardıcıl birləşdirən qırıq xətt

padşah keçdi, heç bir kəsişmə yoxdur. Hansı sahədə olar

bu qırıq xətti məhdudlaşdırmaq? (Hüceyrənin tərəfi 1-dir.)

Seçim düsturundan dərhal belə nəticə çıxır ki, sahə lo-

mana 64/2 − 1 = 31; burada qəfəs düyünləri mərkəzlərdir 64

sahələr və fərziyyə ilə onların hamısı çoxbucaqlının sərhədində yerləşir. Belə ki

Beləliklə, kralın bu cür "trayektoriyaları" kifayət qədər çox olsa da, hamısı

bərabər sahəli çoxbucaqlıları məhdudlaşdırın.

GIA və Vahid Dövlət İmtahanının nəzarət-ölçü materiallarından tapşırıqlar

Tapşırıq B3

Hüceyrə ölçüsü 1 sm 1 sm olan damalı kağızda təsvir edilmiş fiqurun sahəsini tapın (şəklə bax). Cavabınızı kvadrat santimetrlə verin.

4. Nəticə

Tədqiqat prosesində mən istinad, elmi-populyar ədəbiyyatı öyrəndim. Öyrəndim ki, şəbəkənin qovşaqlarında təpələri olan çoxbucaqlının sahəsini tapmaq problemi 1899-cu ildə avstriyalı riyaziyyatçı Pik-i gözəl Pik düsturunu sübut etmək üçün ilhamlandırıb.

İşim nəticəsində damalı kağızda məsələlərin həlli ilə bağlı biliklərimi genişləndirdim, öyrənilən məsələlərin təsnifatını özüm üçün müəyyənləşdirdim və onların müxtəlifliyinə əmin oldum.

Damalı vərəqdə çəkilmiş çoxbucaqlıların sahələrini hesablamağı öyrəndim.Nəzərdə tutulan tapşırıqların çətinlik səviyyəsi fərqlidir - sadədən olimpiadaya qədər. Hər kəs onların arasında mümkün olan mürəkkəblik səviyyəli tapşırıqları tapa bilər, ondan başlayaraq daha çətin olanların həllinə keçmək mümkün olacaqdır.

Belə qənaətə gəldim ki, məni maraqlandıran mövzu kifayət qədər çoxşaxəlidir, damalı kağızda tapşırıqlar müxtəlifdir, onların həlli üsulları və üsulları da müxtəlifdir. Ona görə də bu istiqamətdə işimizi davam etdirmək qərarına gəldim.

5. İstifadə olunmuş ədəbiyyat:

1. N. B. Vasilyev, “Around the Pick formula”, Kvant. - 1974. - No 12

2. Kokse Prasolov VV Planimetriyada tapşırıqlar. - M.: MTsNMO, 2006.t e r G.S.M. Həndəsə giriş. - M.: Nauka, 1966

3. Roslova L.O., Sharygin İ.F. Ölçmələr. - M.: Red. "Açıq dünya", 2005.

İnternet resursları:

:

İşlə bağlı rəy

"Sahələrin hesablanması düz fiqurlar. Seçim üsulu"

Bu mövzunun nəzərdən keçirilməsi yaxşılaşacaq koqnitiv fəaliyyətşagird sonradan həndəsə dərslərində rəsmin harmoniyasını görməyə başlayacaq və həndəsəni (və ümumiyyətlə riyaziyyatı) darıxdırıcı bir elm kimi qəbul etməyi dayandıracaq.

Riyaziyyat müəllimi tərəfindən nəzərdən keçirilir

Xodıreva Tatyana Georgievna

Pik Formula

1. Giriş

2. Pik düsturu. Sübut I.

Sübut II.

Ş.

3. Tapşırıqlar.

4. Təpələrin koordinatları baxımından çoxbucaqlının sahəsi üçün düstur.

5. Tapşırıqlar.

6. Ədəbiyyat

Pik formulu.

1. Giriş.

Tarixdən hikmət çəkirik,

poeziyada - ağıl,

riyaziyyatda - fikir.

F.Bekon

Süjet adi damalı kağız üzərində açılacaq.

Hüceyrələrin yanları boyunca gedən xətlər bir şəbəkə təşkil edir və hüceyrələrin təpələri bu şəbəkənin qovşaqlarıdır. Vərəqə düyünlərində təpələri olan çoxbucaqlı çəkək və onun sahəsini tapaq.

Onu müxtəlif yollarla axtara bilərsiniz. Məsələn, çoxbucaqlını kifayət qədər sadə formalara kəsə, onların sahələrini tapıb əlavə edə bilərsiniz.

Ancaq burada biz çox çətinlik çəkirik. Fiqur asanlıqla düzbucaqlılara, trapesiyaya və üçbucaqlara bölünür və onun sahəsi heç bir çətinlik çəkmədən hesablanır.

Çoxbucaqlı kifayət qədər sadə görünsə də, onun sahəsini hesablamaq çox iş tələb edəcəkdir. Çoxbucaqlı daha cəsarətli görünsə nə olacaq? Belə çıxır ki, təpələri şəbəkənin qovşaqlarında yerləşən çoxbucaqlıların sahələrini daha sadə hesablamaq olar: onların sahəsini çoxbucaqlının daxilində və sərhədində yerləşən qovşaqların sayı ilə əlaqələndirən bir düstur var. Bu gözəl və sadə düstur Pik düsturu adlanır.

2. Pik düsturu.

Çoxbucaqlının təpələri (mütləq qabarıq deyil) tam ədədli qəfəsin qovşaqlarında yerləşir. Onun içərisində şəbəkənin B düyünləri, G düyünlərinin sərhədində yerləşir. Onun sahəsinin B + olduğunu sübut edək – 1 (Pik düsturu).

Sübut I.

Təpələri tam ədəd qəfəsinin qovşaqlarında olan, yəni tam ədəd koordinatlarına malik olan çoxbucaqlıya nəzər salın.

Çoxbucaqlıları qəfəsin qovşaqlarında təpələri olan üçbucaqlara bölürük, nə içərisində, nə də yanlarında düyünlər yoxdur.

İşarə et:

nçoxbucaqlının tərəflərinin sayıdır,

m qəfəsin qovşaqlarında təpələri olan üçbucaqların sayı, içərisində və ya tərəflərində qovşaqları olmayan,

B çoxbucaqlı daxilində qovşaqların sayı,

Г təpələri də daxil olmaqla tərəflərdəki qovşaqların sayıdır.

Bütün bu üçbucaqların sahələri eyni və bərabərdir.

Beləliklə, çoxbucaqlının sahəsi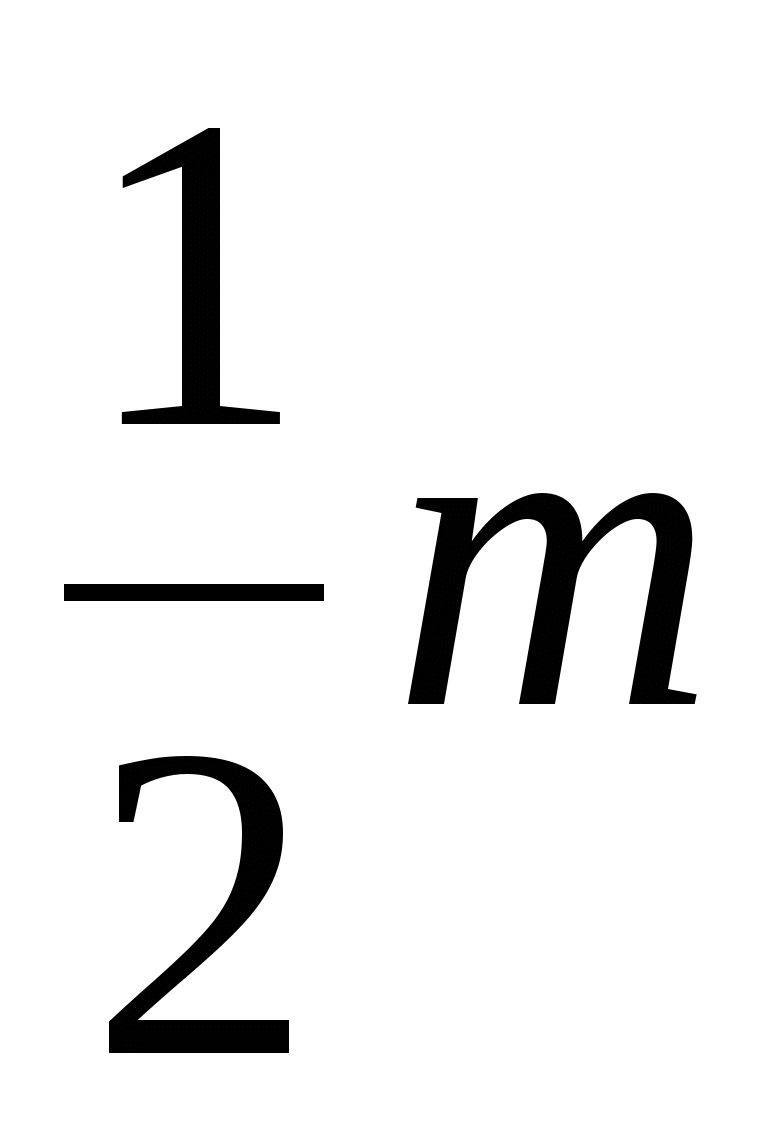
.

180 0 m .

İndi bu məbləği başqa cür tapaq.

İstənilən daxili qovşaqda təpəsi olan bucaqların cəmi 360 0-dır.

Onda bütün daxili qovşaqlarda təpələri olan bucaqların cəmi 360 0 V-dir.

Təpələrdə deyil, yanlardakı düyünlərdəki bucaqların ümumi cəmi 180 0-dır (G - n).

Çoxbucaqlının təpələrindəki bucaqların cəmi 180 0 ( n – 2) .

Bütün üçbucaqların bucaqlarının ümumi cəmidir 360 0 V + 180 0 (G - n) + 180 0 (n – 2).

Beləliklə, 180 0 m\u003d 360 0 V + 180 0 (G - n) + 180 0 (n – 2),

180 0 m\u003d 360 0 V + 180 0 G - 180 0 n + 180 0 n– 180 0 2,

180 0 m\u003d 360 0 V + 180 0 G– 360 0,

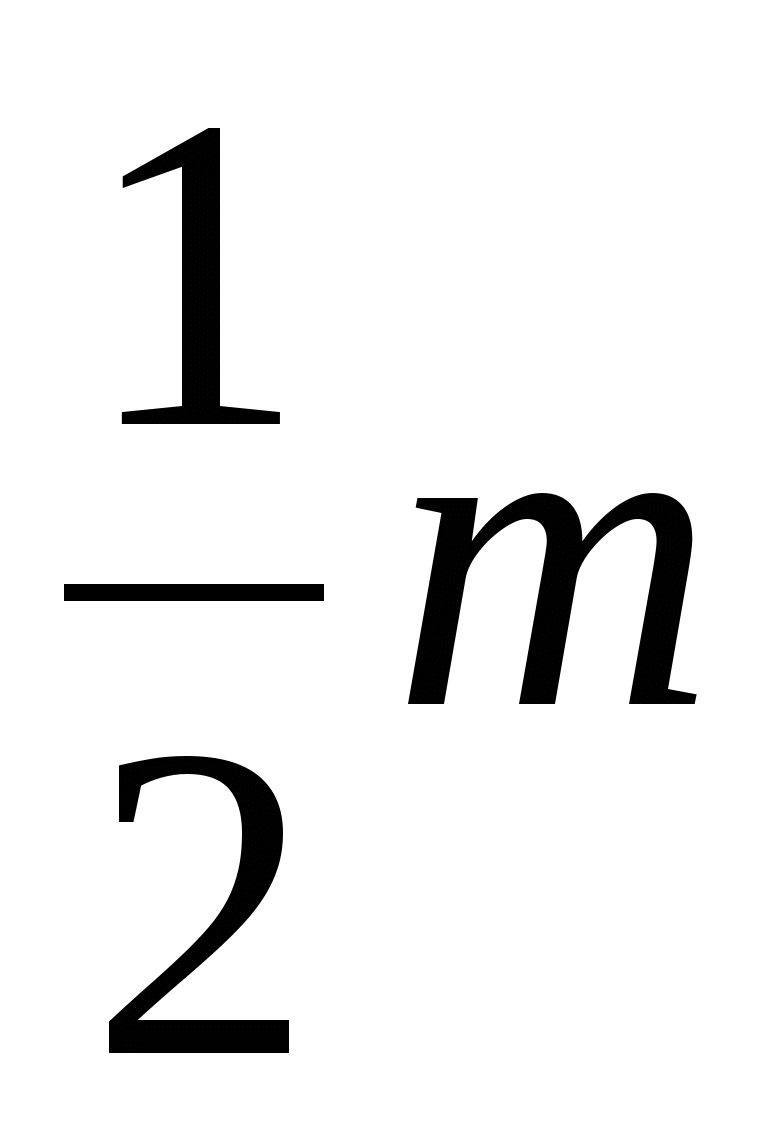= B + – 1 ,

buradan çoxbucaqlının S sahəsi üçün ifadəni alırıq:

S= B + – 1 ,

Pik düsturu kimi tanınır.

Şəkildə: V = 24, D = 9, buna görə də,S = 24 + – 1 = 27,5.

Peak düsturundan istifadə edərək birinci çoxbucağın sahəsini tapın:

B = 28 (yaşıl nöqtələr);

D = 20 (mavi nöqtələr).

Alırıq, S =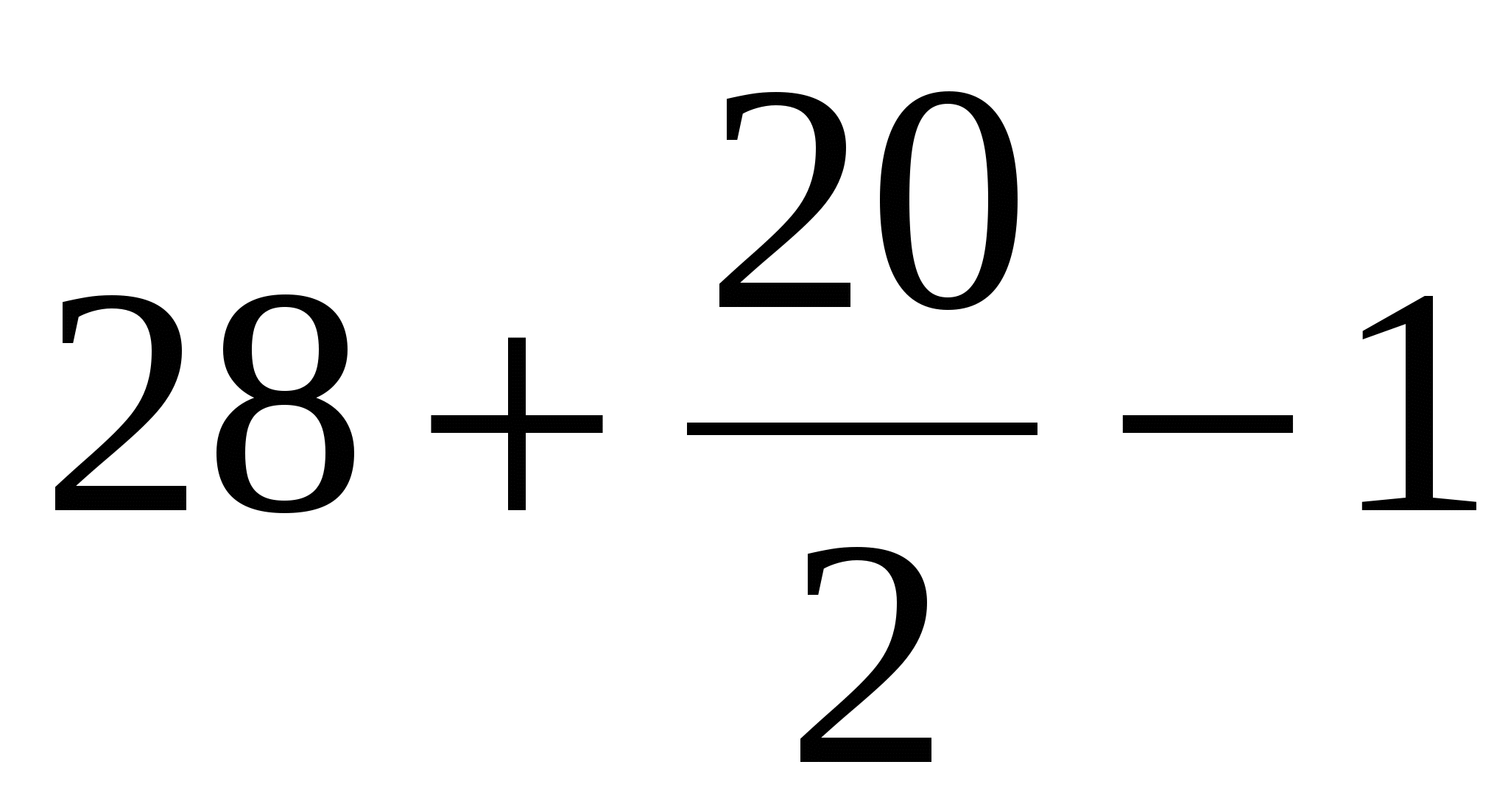
= 37 kvadrat vahid

Sübut II.

Tam ədəd şəbəkəsinin qovşaqlarında təpələri olan hər bir M çoxbucaqlıya f (M) = ədədini təyin edirik.
, burada cəmlənmə M-ə aid bütün qəfəs qovşaqları üzərindədir və bucaq aşağıdakı kimi müəyyən edilir: =
çoxbucaqlının daxili nöqtəsi üçün, =
təpədən başqa sərhəd nöqtəsi üçün və – təpəsindəki bucaq, əgər verilmiş düyün təpədirsə. F (M) = olduğunu görmək asandır
+
= B + – 1. F (M) ədədinin M çoxbucağının sahəsinə bərabər olduğunu yoxlamaq qalır.

M çoxbucaqlı şəbəkənin düyünlərində təpələri olan M 1 və M 2 çoxbucaqlılarına kəsilsin. Onda f(M) = f(M 1) + f(M 2) olur, çünki hər düyün üçün bucaqlar toplanır. Deməli, M, M 1 və M 2 çoxbucaqlılarından ikisi üçün Pik düsturu doğrudursa, üçüncüsü üçün də doğrudur.

M tərəfləri olan düzbucaqlıdırsa səh və q, qəfəs xətləri boyunca yönəldilmiş, sonra

f (M) = (p – 1)(q – 1) +
= pq.

Bu halda Pik düsturu etibarlıdır. M düzbucağını diaqonal olaraq M 1 və M 2 üçbucaqlarına kəsərək və f (M) = f (M 1) + f (M 2) və f (M 1) = f (M 2) faktından istifadə edərək, bunu etmək asandır. qəfəsin xətləri boyunca istiqamətlənmiş ayaqları olan istənilən düzbucaqlı üçbucaq üçün Pik düsturunun doğruluğunu sübut etmək. Düzbucaqlıdan bir neçə belə üçbucağı kəsməklə istənilən üçbucaq əldə etmək olar.

Pik düsturunun sübutunu tamamlamaq üçün qeyd etmək lazımdır ki, istənilən çoxbucaqlı kəsişməyən diaqonallarla üçbucaqlara kəsilə bilər.

Ş.

Fiqurun sahəsi ilə bu rəqəmə düşən qovşaqların sayı arasındakı əlaqə düzbucaqlı vəziyyətində xüsusilə aydındır.

Qoy A B C D- şəbəkə xətləri boyunca gedən qovşaqlarda və tərəflərdə təpələri olan düzbucaqlı.

ilə işarələyin AT düzbucaqlı içərisində yatan qovşaqların sayı və vasitəsilə G onun sərhədindəki qovşaqların sayıdır. Şəbəkəni yarım xana sağa və yarım xana aşağıya köçürün.

Sonra düzbucaqlının ərazisi qovşaqlar arasında aşağıdakı kimi "paylana" bilər: hər biri AT qovşaqlar hər biri dəyişdirilmiş şəbəkənin bütün hüceyrəsini "nəzarət edir" G- 4 sərhəd olmayan künc qovşağı - hüceyrənin yarısı və künc nöqtələrinin hər biri - hüceyrənin dörddə biri. Beləliklə, düzbucaqlının sahəsi S-dir

Beləliklə, qovşaqlarda təpələri olan düzbucaqlılar və şəbəkə xətləri boyunca gedən tərəflər üçün düstur qurduq.

Bu düsturun təkcə düzbucaqlılar üçün deyil, həm də tor qovşaqlarında təpələri olan ixtiyari çoxbucaqlılar üçün də doğru olduğunu sübut edək.

ilə işarələyin S m poliqon sahəsiM qovşaqlarda təpələri ilə və vasitəsiləP m - dəyər
, haradaAT m daxili qovşaqların sayıdırM, a G m sərhəddəki qovşaqların sayıdır. Sonra Pick düsturu kimi yazıla bilər
.

Düsturun sübutunu bir neçə mərhələyə bölürük.

Addım 1.

Əgər çoxbucaqlıM 2 çoxbucaqlıya kəsilmiş grid qovşaqlarında təpələri iləM 1 və M 2 , həmçinin yalnız grid qovşaqlarında təpələri olan, sonra
. Çoxbucaqlı olsunM çoxbucaqlılara kəsinM 1 və M 2 seqment tərəfindən düyünlərdə təpələri ilə AB. Seqmentə düşənlərdən başqa bütün qovşaqlarAB, formulun sol və sağ hissələrinə eyni töhfəni verin. AB seqmentində yerləşən düyünləri nəzərdən keçirək.

Əgər belə bir düyün A və B arasında yerləşirsə (məsələn, C), onda çoxbucaqlı üçünM daxilidir və çoxbucaqlılar üçünM 1 və M 2 - sərhəd. Bu səbəbdən onun töhfəsiP m 1-ə bərabərdir və ifadələrin hər birində
və
– hər biri 0,5, yəni belə bir qovşağın töhfələriP m və
bərabərdirlər.

A və B qovşaqlarını nəzərdən keçirək. Onlar hər ikisi üçün sərhəddir M, və üçün M 1 , M 2 .

Buna görə də bu qovşaqların hər birinin qatqısıP m 0,5 a təşkil edir
- vahid. Bu, A və B qovşaqlarının ümumi töhfəsi deməkdirP m 1-ə bərabərdir ki, bu da onların töhfəsindən 1 azdır
. Amma
, a .

Bütün qovşaqların ümumi "töhfəsindən" P m 1-dən çıxarılır
2 çıxarılır və bu, A və B qovşaqlarının töhfələrindəki fərqi kompensasiya edir.

Belə ki,
.

Addım 2

Əgər çoxbucaqlı M iki çoxbucaqlıya kəsilmiş grid qovşaqlarında təpələri ilə M 1 və M 2 (həmçinin düyünlərdə təpələri ilə) və düstur bəzi iki çoxbucaqlı üçün doğrudur MM 1 , M 2 , onda üçüncü çoxbucaqlı üçün də doğrudur.

Məsələn, bunun üçün doğrudurM 1 və M 2 , yəni
. Sonra (ilk addımda), amma ilk addım), sonuncu ifadə bərabərdirP m , və bərabərlik
və Seçim düsturu var.

Addım 3

Təpələri tor qovşaqlarında və ayaqları tor xətlərində uzanan düzbucaqlı üçbucaq üçün Pik düsturunu sübut edək.

Üçbucaq ABC düzbucaqlı şəklində qurun A B C D .

Düzbucaqlılar üçün Pik düsturu düzgündür: S A B C D = P A B C D . İlk addıma görə P A B C D = P ABC + P ACD , P ABC = P ACD , belə ki P A B C D = 2P ABC . Amma S A B C D = 2 S ABC . Buna görə də S ABC = P ABC .

Addım 4

Pik düsturu şəbəkə qovşaqlarında təpələri olan ixtiyari üçbucaq üçün düzgündür.

Şəkli araşdırdıqdan sonra başa düşmək asandır: hər hansı belə üçbucağı şəbəkə xətləri boyunca uzanan tərəfləri olan bir neçə düzbucaqlıdan, bir neçə düzbucaqlıdan və tor xətlərində ayaqları olan düzbucaqlı üçbucaqdan “kəsməklə” əldə etmək olar. Pik düsturu düzbucaqlılar və düzbucaqlı üçbucaqlar üçün doğru olduğu üçün (2-ci addımı yadda saxla) ilkin üçbucaq üçün də doğrudur.

Sübut etdik ki, çoxbucaqlı torun qovşaqlarında təpələri olan üçbucaqlara kəsilə bilərsə, Pik düsturu onun üçün doğrudur.

3. Tapşırıqlar.

Fiqurların sahəsini tapın:

1
.

B=9

G = 4

B=9

G = 5

Əsərin mətni şəkillər və düsturlar olmadan yerləşdirilib.
Tam versiyası iş PDF formatında "İş faylları" sekmesinde mövcuddur

Giriş

Mən 6-cı sinif şagirdiyəm. Keçən ildən həndəsə öyrənməyə başladım, çünki məktəbdə “Riyaziyyat. Hesab. Həndəsə” redaktoru E.A. Bunimoviç, L.V.Kuznetsova, S.S. Minaeva və başqaları.

Ən çox diqqətimi “Fiqurların kvadratları”, “Düsturların tərtibi” mövzuları cəlb etdi. Diqqət etdim ki, eyni fiqurların sahələri müxtəlif yollarla tapıla bilər. Gündəlik həyatda tez-tez ərazi tapmaq problemi ilə qarşılaşırıq. Məsələn, rənglənəcək döşəmə sahəsini tapın. Maraqlıdır, axırda təmir üçün lazımi miqdarda divar kağızı almaq üçün otağın ölçüsünü bilməlisiniz, yəni. divar sahəsi. Kvadrat, düzbucaqlı və düzbucaqlı üçbucağın sahəsini hesablamaq mənə heç bir çətinlik yaratmadı.

Bu mövzu ilə maraqlandım, internetdə əlavə material axtarmağa başladım. Axtarış nəticəsində Pick düsturuna rast gəldim - bu damalı kağıza çəkilmiş çoxbucaqlının sahəsini hesablamaq üçün bir düsturdur. Bu düsturdan istifadə edərək ərazinin hesablanması mənə hər bir tələbə üçün əlçatan görünürdü. Buna görə qərar verdim tədqiqat işi.

Mövzunun aktuallığı:

Bu mövzu həndəsə kursunun öyrənilməsinin əlavə və dərinləşdirilməsidir.

Bu mövzunun öyrənilməsi olimpiadalara və imtahanlara daha yaxşı hazırlaşmağa kömək edəcək.

Məqsəd:

Seçim düsturu ilə tanış olun.

Usta qərar vermə həndəsi məsələlər Pik düsturundan istifadə etməklə.

Nəzəri və praktiki materialları sistemləşdirin və ümumiləşdirin.

Tədqiqat məqsədləri:

Problemlərin həllində düsturun tətbiqinin effektivliyini və məqsədəuyğunluğunu yoxlayın.

Seçim düsturunu müxtəlif mürəkkəblik problemlərinə necə tətbiq edəcəyinizi öyrənin.

Seçmə düsturundan və ənənəvi üsuldan istifadə edərək həll olunan problemləri müqayisə edin.

Əsas hissə

1.1. Tarixə istinad

Georg Alexander Pick 10 avqust 1859-cu ildə anadan olan Avstriyalı riyaziyyatçıdır. O idi istedadlı uşaq, ona özəl instituta rəhbərlik edən atası dərs deyirdi. 16 yaşında Georg orta məktəbi bitirdi və Vyana Universitetinə daxil oldu. 20 yaşında fizika və riyaziyyatdan dərs demək hüququ qazandı. Çoxbucaqlılar şəbəkəsinin sahəsini təyin etmək düsturu ona dünya şöhrəti gətirdi. Düsturunu 1899-cu ildə bir məqaləsində dərc etdi. Polşa alimi Hugo Steinhaus 1969-cu ildə onu riyazi şəkillərin nəşrinə daxil edəndə məşhurlaşdı.

Georg Pieck Vyana Universitetində təhsil alıb və 1880-ci ildə doktorluq dissertasiyasını bitirib. Doktorluq dərəcəsini aldıqdan sonra Praqadakı Şerl-Ferdinand Universitetində Ernest Machın assistenti vəzifəsinə təyin olunub. Orada müəllim oldu. 1927-ci ildə təqaüdə çıxana qədər Praqada qaldı və sonra Vyanaya qayıtdı.

Pik 1911-ci ildə Eynşteyni riyazi fizika professoru təyin edən Alman Praqa Universitetində komitəyə sədrlik etdi.

O, Çexiya Elmlər və İncəsənət Akademiyasının üzvü seçildi, lakin Praqanın faşistlər tərəfindən ələ keçirilməsindən sonra ölkədən çıxarıldı.

1938-ci il martın 12-də nasistlər Avstriyaya daxil olduqdan sonra o, Praqaya qayıtdı. 1939-cu ilin martında faşistlər Çexoslovakiyaya hücum etdilər. 1942-ci il iyulun 13-də Pik Şimali Çexiyada nasistlərin qurduqları Teresyenştadt düşərgəsinə deportasiya edildi və orada iki həftə sonra 82 yaşında öldü.

1.2. Araşdırma və sübut

Tədqiqat işimə sual verməklə başladım: fiqurların hansı sahələrini tapa bilərəm? Müxtəlif üçbucaqların və dördbucaqlıların sahəsini hesablamaq üçün düstur yarada bilərdim. Bəs beş, altı və ümumiyyətlə çoxbucaqlılar haqqında nə demək olar?

Müxtəlif saytlarda araşdırma zamanı beş, altı və digər çoxbucaqlıların sahəsini hesablamaq üçün problemlərin həlli yollarını gördüm. Bu məsələlərin həlli düsturu Pik düsturu adlanırdı. O, belə görünür :S =B+G/2-1, harada AT- çoxbucaqlı içərisində yerləşən qovşaqların sayı, G- çoxbucaqlının sərhədində yerləşən qovşaqların sayı. Bu düsturun özəlliyi ondan ibarətdir ki, onu yalnız damalı kağıza çəkilmiş çoxbucaqlılara tətbiq etmək olar.

İstənilən belə çoxbucaqlı asanlıqla şəbəkənin qovşaqlarında təpələri olan üçbucaqlara bölünə bilər, içərisində və ya yanlarında heç bir qovşaq yoxdur. Göstərilə bilər ki, bütün bu üçbucaqların sahələri eyni və ½-ə bərabərdir və buna görə də çoxbucaqlının sahəsi onların sayının yarısına bərabərdir. T.

Bu ədədi tapmaq üçün çoxbucaqlının tərəflərinin sayını n ilə işarə edirik AT- içindəki qovşaqların sayı, vasitəsilə G təpələr daxil olmaqla, tərəflərdəki qovşaqların sayıdır. Bütün üçbucaqların bucaqlarının cəmi 180°-dir. T.

İndi isə cəmini başqa cür tapaq.

İstənilən daxili qovşaqda təpəsi olan bucaqların cəmi 2,180°-dir, yəni. bucaqların ümumi cəmi 360°-dir. AT; təpələrdə deyil, tərəflərdəki düyünlərdəki bucaqların ümumi cəmi ( Cənab n)180°, və çoxbucaqlının təpələrindəki bucaqların cəmi ( G- 2)180°. Bu minvalla, T= 2.180°. B+(G-n)180°+(n -2)180 °. Mötərizənin açılması və 360°-yə bölünməsi çoxbucaqlının S sahəsi üçün Pik düsturu kimi tanınan düsturu verir.

2. Praktiki hissə

Bu düsturu OGE-2017 kolleksiyasından tapşırıqlar üzərində yoxlamaq qərarına gəldim. Üçbucağın, dördbucağın və beşbucağın sahəsini hesablamaq üçün tapşırıqlar aldım. Cavabları iki yolla həll edərək müqayisə etmək qərarına gəldim: 1) Fiqurları düzbucaqlıya əlavə etdim və yaranan düzbucaqlının sahəsindən düzbucaqlı üçbucaqların sahəsini çıxardım; 2) Peak formulunu tətbiq etdi.

S = 18-1.5-4.5 = 12 və S = 7+12/2-1= 12

S = 24-9-3 = 12 və S = 7+12/2-1 = 12

S = 77-7.5-12-4.5-4 = 49 və S = 43+14/2-1 = 49

Nəticələri müqayisə edərək belə qənaətə gəlirəm ki, hər iki düstur eyni cavabı verir. Pik düsturundan istifadə edərək fiqurun sahəsini tapmaq daha sürətli və asan oldu, çünki hesablamalar daha az idi. Qərarın asanlığı və hesablamalarda vaxta qənaət gələcəkdə OGE-dən keçərkən mənim üçün faydalı olacaq.

Bu, məni daha mürəkkəb fiqurlara Seçim düsturunu tətbiq etmək imkanını sınamağa vadar etdi.

S = 0 + 4/2 -1 = 1

S \u003d 5 + 11 / 2-1 \u003d 9,5

S=4+16/2-1=1

Nəticə

Pick formulunu başa düşmək və istifadə etmək asandır. Birincisi, saymaq, 2-yə bölmək, toplamaq və çıxmaq kifayətdir. İkincisi, çox vaxt sərf etmədən ərazini və mürəkkəb rəqəmi tapa bilərsiniz. Üçüncüsü, bu düstur istənilən çoxbucaqlı üçün işləyir.

Dezavantaj odur ki, Seçmə Düsturu yalnız damalı kağızda çəkilmiş və təpələri hüceyrələrin düyünlərində olan fiqurlara şamil edilir.

Əminəm ki, buraxılış imtahanlarını verərkən rəqəmlərin sahəsini hesablamaqla bağlı problemlər çətinlik yaratmayacaq. Axı mən Pick düsturu ilə artıq tanışam.

Biblioqrafiya

Bunimoviç E.A., Dorofeev G.V., Suvorova S.B. s. Riyaziyyat. Hesab. Həndəsə. 5-ci sinif: dərslik. ümumi təhsil üçün proqramı olan təşkilatlar. elektrona. daşıyıcı -3-cü çap.-M.: Maarifçilik, 2014.- 223, s. : xəstə. - (Sferalar).

Bunimoviç E.A., Kuznetsova L.V., Minaeva S.S. s. Riyaziyyat. Hesab. Həndəsə. 6-cı sinif: dərslik. ümumi təhsil üçün təşkilatlar-5-ci nəşr.-M.: Təhsil, 2016.-240-lar. : xəstə.- (Sferalar).

Vasiliev N.B. Seçim düsturunun ətrafında. //Kvant.- 1974.-№2. -səh.39-43

Rəssolov V.V. Planimetriyada problemlər. / 5-ci nəşr, düzəliş. Və əlavə. - M.: 2006.-640-cı illər.

İ.V. Yaschenko.OGE. Riyaziyyat: tipik imtahan variantları: O-39 36 variant - M .: Milli Təhsil Nəşriyyatı, 2017. -240 s. - (OGE. FİPİ-məktəbi).

"OGE həll edəcəm": riyaziyyat. Dmitri Qushchinin təlim sistemi. OGE-2017: tapşırıqlar, cavablar, həllər [Elektron resurs]. Giriş rejimi: https://oge.sdamgia.ru/test?id=6846966 (Giriş tarixi 04/02/2017)

Damalı kağızda çoxbucaqlının sahəsini qiymətləndirmək üçün bu poliqonun neçə hüceyrəni əhatə etdiyini hesablamaq kifayətdir (hüceyrənin sahəsini vahid kimi götürürük). Daha doğrusu, əgər Sçoxbucaqlının sahəsidir, tamamilə çoxbucaqlının daxilində yerləşən hüceyrələrin sayıdır və çoxbucaqlının daxili hissəsi ilə ən azı bir ümumi nöqtəsi olan hüceyrələrin sayıdır.

Aşağıda yalnız bütün təpələri damalı kağızın qovşaqlarında - tor xətlərinin kəsişdiyi yerlərdə olan çoxbucaqlıları nəzərdən keçirəcəyik. Belə çıxır ki, belə çoxbucaqlılar üçün aşağıdakı düstur təyin edə bilərsiniz:

ərazi haradadır, rçoxbucaqlı daxilində ciddi şəkildə yatan qovşaqların sayıdır.

Bu düstur 1899-cu ildə onu kəşf edən riyaziyyatçının şərəfinə “Pik düsturu” adlanır.

sadə üçbucaqlar

Damalı kağıza çəkilmiş hər hansı üçbucağın sahəsi onu düzbucaqlı üçbucaqların və tərəfləri çəkilmiş üçbucağın təpələrindən keçən tor xətlərini izləyən düzbucaqlıların sahələrinin cəmi və ya fərqi kimi təqdim etməklə asanlıqla hesablana bilər. Bunu etdikdən sonra, məsələn, Şəkil 1.34-də göstərilən üçbucaqlar üçün sahənin həmişə "qəbul edilmiş" rəqəmə - formanın nömrəsinə bərabər olduğuna əmin ola bilərsiniz, burada tam ədəddir.

Təpə nöqtələri istisna olmaqla, nə daxilində, nə də yanlarında heç bir tor qovşaqları yoxdursa, üçbucağı sadə adlandıraq. Şəkildəki bütün sadə üçbucaqlar. 1.34 sahə var. Bunun təsadüfi olmadığını görəcəyik.

Bir tapşırıq. Zamanın ilkin anında üç çəyirtkə (üç nöqtə) bir hücrənin üç təpəsində oturur və sonra "sıçrayış oynamağa" başlayır: hər biri digər ikisindən birinin üstündən tullana bilər, bundan sonra simmetrik bir nöqtədə bitir. ona (Şəkil 1.35, aydındır ki, istənilən sayda belə atlamalardan sonra çəyirtkələr damalı kağız düyünlərinə düşəcək). Çəyirtkələr bir neçə atlamadan sonra hansı üçlük nöqtələrdə ola bilər?

Üç çəyirtkə ilkin olaraq eyni hüceyrənin üç təpəsində olan təpələrində eyni vaxtda görünə bilsə, üçbucağı əlçatan adlandırırıq; biz təpələrdən birinin digər iki təpədən hər hansı birinə nisbətən simmetrik olan nöqtəyə getməsindən ibarət olan üçbucağın çevrilməsini sıçrayış adlandıracağıq (bu iki təpə yerində qalır).

Teorem 1. Damalı kağız düyünləri olan üçbucaqların aşağıdakı üç xüsusiyyəti bir-birinə bərabərdir:

1) üçbucağın sahəsi var,

2) üçbucaq sadədir,

3) üçbucaq əlçatandır.

Sadə üçbucağın bu teoremin doğruluğuna səbəb olan aşağıdakı xassələri ilə tanış olaq.

1. Atılan zaman üçbucağın sahəsi dəyişmir.

2. İstənilən əlçatan üçbucağın sahəsi var.

3. Sadə üçbucağı tamamlasanız ABC paraleloqrama A B C D, onda bu paraleloqramın nə daxilində, nə də yanlarında (təpələri saymadan) düyünlər olmayacaq.

4. Sadə üçbucaqdan tullanan zaman sadə birini alırsınız.

5. Sadə üçbucaqdan bucaqlardan biri küt və ya düzdür (üstəlik, sonuncu hal yalnız üç təpəsi eyni xanaya aid olan üçbucaq üçün mümkündür, tərəfləri 1, 1 minimal olan belə sadə üçbucağı adlandıracağıq. )

6. İstənilən sadə qeyri-minimal üçbucaqdan, ən böyük tərəfi orijinal tərəfin ən böyük tərəfindən kiçik olan üçbucağı almaq üçün tullana bilər.

7. İstənilən sadə üçbucağı sonlu sayda atlama ilə minimuma çevirmək olar.

8. İstənilən sadə üçbucaq əlçatandır.

9. İstənilən sadə üçbucağın sahəsi var.

10. İstənilən üçbucaq sadə olanlara kəsilə bilər.

11. İstənilən üçbucağın sahəsi bərabərdir və onu sadə olanlara kəsmək üçün onların sayı bərabərdir. m.

12. İstənilən sahə üçbucağı sadədir.

13. İstənilən iki qovşaq üçün AMMA və AT aralarında başqa qovşaqların olmadığı seqmentdəki qəfəslər, bir node var FROM belə ki, üçbucaq ABC- sadə.

14. Düyün FROMəvvəlki əmlak, siz həmişə seçə bilərsiniz ki, bucaq DİA küt və ya düz olun.

15. Damalı müstəvi kəsilsin bərabər paraleloqramlar belə ki, bütün qovşaqlar paraleloqramların təpələri olsun. Onda bu paraleloqramlardan birinin diaqonalı ilə kəsildiyi üçbucaqların hər biri sadədir.

16. (Əks 15). Üçbucaq ABC o zaman sadədir ki, bütün mümkün üçbucaqlar əldə edilir ABC nodu köçürən paralel köçürmələr AMMA qəfəsin müxtəlif qovşaqlarına, üst-üstə düşməyin.

17. Şəbəkə - damalı kağız qovşaqları hüceyrələrlə dörd alt qəfəsə bölünürsə (şəkil 1.36), onda sadə üçbucağın təpələri mütləq üç müxtəlif alt qəfəsə düşəcək (hər üçünün müxtəlif təyinatları var).

Növbəti iki xüsusiyyət üç çəyirtkə probleminin cavabını verir.

18. Üç çəyirtkə eyni vaxtda sadə üçbucağın təpələri rolunu oynayan və ilkin üçbucağın müvafiq təpələri ilə eyni işarəyə malik olan üçlü nöqtələri vura bilər.

19. İki çəyirtkə eyni vaxtda digər qovşaqların olmadığı seqmentdə müvafiq işarələrin həmin cüt qovşaqlarını vura bilər.

Çoxbucaqlı üçbucaqlı

Dəyərləri Seçim düsturunda uyğun olan damalı kağızda çoxbucaqlıların müəyyən bir formasını nəzərdən keçirəcəyik. Ancaq bu xüsusi vəziyyətdən, ixtiyari çoxbucaqlı üçbucaqlara kəsmək teoremindən istifadə edərək birbaşa ən ümumi birinə keçə bilərsiniz (damalı kağız artıq lazım deyil).

Müstəvidə bəzi çoxbucaqlı və bəzi sonlu çoxluq verilsin Kiməçoxbucaqlının daxilində və onun sərhəddində yerləşən nöqtələr (bundan əlavə, çoxbucaqlının bütün təpələri çoxluğa aiddir. Kimə).

Təpələri ilə üçbucaqlaşdırma Kimə verilmiş çoxbucaqlının çoxluqda təpələri olan üçbucaqlara bölünməsi adlanır Kimə ki, hər bir nöqtə Kimə bu nöqtənin aid olduğu üçbucaq üçbucaqlarının hər biri üçün təpə kimi xidmət edir (yəni, Kiməüçbucaqların içərisinə və ya yanlarına düşməyin, şək. 1.37).

Teorem 2. a) hər hansı n-gon diaqonallarla üçbucaqlara kəsilə bilər və üçbucaqların sayı bərabər olacaqdır n- 2 (bu bölmə təpələrdə təpələri olan üçbucaqdır n-gon).

b) Qoy r nöqtələr (bütün təpələr daxil olmaqla), içəridə - daha çox i xal. Sonra işarələnmiş nöqtələrdə təpələri olan bir üçbucaq var və belə bir üçbucaqlı üçbucaqların sayı bərabər olacaqdır.

Təbii ki, a) b) zamanın xüsusi halıdır.

Bu teoremin etibarlılığı aşağıdakı müddəalardan irəli gəlir.

1) Ən böyük bucağın yuxarısından n-gon () siz həmişə çoxbucaqlının içərisində olan diaqonal çəkə bilərsiniz.

2) Əgər n-çapraz olaraq kəsilir R-gon və q-onda.

3) Bucaqların cəmi n-gon bərabərdir.

4) Hər hansı n-qon diaqonal olaraq üçbucaqlara kəsilə bilər.

5) İçərisində və sərhədində bir neçə nöqtə (o cümlədən onun hər üç təpəsi də daxil olmaqla) işarələnmiş hər hansı üçbucaq üçün işarələnmiş nöqtələrdə təpələri olan üçbucaq var.

6) Eyni şey hər hansı bir şəxs üçün keçərlidir n-gon.

7) Üçbucaqlı üçbucaqların sayı, haradadır i və r- çoxbucaqlının daxilində və sərhədində müvafiq olaraq işarələnmiş nöqtələrin sayı. Bölməni çağıraq n Bölmə çoxbucaqlılarından birinin hər bir təpəsi aid olduğu bütün digər bölmə çoxbucaqlılarının təpəsi kimi xidmət edərsə, bir neçə çoxbucaqlıya -qonşu düzgündür. 8) Əgər təpələrdən k düzgün şəkildə bölündüyü -gons n-gon, i təpələr içəridə yerləşir və r- sərhəddə n-gon, sonra nömrə k-gons bərabərdir

9) Əgər təyyarənin nöqtələri və bu nöqtələrdə ucları olan seqmentlər çoxbucaqlıya düzgün bölünmüş çoxbucaqlı əmələ gətirirsə, onda (şək. 1.38)

Seçim düsturu 1 və 2-ci teoremlərdən ibarətdir:

1.5 Düzbucaqlı üçbucağın ayaqları üzərində qurulmuş kvadratların sahələrinin cəminə dair Pifaqor teoremi

Teorem. Düzbucaqlı üçbucağın ayaqları üzərində qurulmuş kvadratların sahələrinin cəmi bu üçbucağın hipotenuzası üzərində qurulmuş kvadratın sahəsinə bərabərdir.Sübut. Qoy ABC(Şəkil 1.39) düzbucaqlı üçbucaqdır və BDEA, AFGE və BCKH- ayaqları və hipotenuzası üzərində qurulmuş kvadratlar; ilk iki kvadratın sahələrinin cəminin üçüncü kvadratın sahəsinə bərabər olduğunu sübut etmək tələb olunur.

sərf edək Günəş. Sonra kvadrat BCKH iki düzbucaqlıya bölün. Düzbucaqlı olduğunu sübut edək BLMH kvadrata bərabərdir BDEA, və düzbucaqlı LCKM kvadrata bərabərdir AFGC.

Köməkçi xətləri çəkin DC və AN. Üçbucaqları nəzərdən keçirin DCB və ABH. Üçbucaq DCBəsasının olması BD, kvadrat ilə ümumi BDEA, və hündürlük CN, hündürlüyə bərabərdir AB bu kvadrat kvadratın yarısına bərabərdir. Üçbucaq AVNəsasının olması VN, düzbucaqlı ilə ümumi BLMH, və hündürlük AR, hündürlüyə bərabərdir BL bu düzbucaqlının yarısı onun yarısına bərabərdir. Bu iki üçbucağı bir-biri ilə müqayisə etdikdə onların olduğunu görürük BD = VA və BC = HH(kvadratın tərəfləri kimi);

Bundan daha çox, DCB = AVN, çünki bu bucaqların hər biri ümumi hissədən ibarətdir - ABC və düz bucaq. Beləliklə, üçbucaqlar AVN və BCD bərabərdirlər. Buradan belə çıxır ki, düzbucaqlı BLMN kvadrata bərabərdir BDEA. Eyni şəkildə düzbucaqlı olduğu sübut edilmişdir LGKM kvadrata bərabərdir AFGC. Bundan belə çıxır ki, kvadrat FAPC kvadratların cəminə bərabərdir BDEA və AFGC.

Təqdimatların önizləməsindən istifadə etmək üçün Google hesabı (hesab) yaradın və daxil olun: https://accounts.google.com

Slayd başlıqları:

7 nömrəli tam orta məktəbin 8 "A" sinif şagirdi Yunosheva Kseniya Təlimatçı: Babina Natalya Alekseevna Salsk 2011 "Pik Formula"

İşin məqsədləri: Bir qəfəsli çoxbucaqlının sahəsini tapmaq üçün düsturun, məktəb proqramından fərqli olan başqasının mövcudluğunu tapmaq. İstənilən formulun tətbiqi sahələri.

Giriş. Riyaziyyat təhsili almışdır ümumtəhsil məktəbləri, ən mühüm komponentdir ümumi təhsil və ümumi mədəniyyət müasir insan. Bu mərhələdə, məktəb sistemi on bir illik təhsil üçün nəzərdə tutulmuşdur. On birinci sinfin sonunda bütün şagirdlər məktəbdə oxuyarkən əldə etdikləri biliklərin səviyyəsini göstərəcək Vahid Dövlət İmtahanını verməlidirlər. Lakin məktəb kurikulumu heç də həmişə hər hansı problemin həlli üçün ən rasional yolları təqdim etmir. Məsələn, baxır Nəticələrdən istifadə edin 2010-cu il göstərir ki, bir çox tələbələr B6 tapşırığına görə xal itirirlər. Mən vaxta qənaət etmək və bu problemi düzgün həll etmək üçün yola çıxdım.

Tapşırıq B6. Şəkillər 1 sm x 1 sm ölçülü hüceyrələrlə damalı kağızda təsvir edilmişdir (şəklə bax). Onların sahəsini kvadrat santimetrdə tapın.

Beləliklə, hələ də bu tapşırığı həll etmək üçün 8-ci sinifdə oxuduğumuz ərazinin tapılması üçün düsturları tətbiq etməliyəm. Amma bu, çox vaxt aparacaq və suala mümkün qədər tez cavab verməliyəm, çünki imtahan vaxtı ciddi şəkildə məhduddur. Ona görə də araşdırma apardıqdan sonra öyrəndim ki, Pik teoremi var ki, məktəb proqramında öyrənilməmiş, amma tapşırığın öhdəsindən daha tez gəlməyə kömək edəcək.

Tarixə istinad. Georg Alexander Pick (10 avqust 1859 - 26 iyul 1942) Avstriyalı riyaziyyatçı idi. Terezin həbs düşərgəsində öldü. Bu gün çoxbucaqlılar şəbəkəsinin sahəsini təyin etmək üçün Pik düsturuna görə tanınır. O, düsturunu 1899-cu ildə bir məqalədə nəşr etdi, Hugo Steinhaus onu 1969-cu ildə Mathematical Pictures nəşrinə daxil etdikdən sonra məşhurlaşdı. Pik Vyana Universitetində oxumuş və 1880-ci ildə doktorluq dərəcəsini tamamlamışdır. Doktorluq dərəcəsini aldıqdan sonra Praqadakı Şerl-Ferdinand Universitetində Ernest Machın assistenti vəzifəsinə təyin olunub. 1881-ci ildə orada müəllim oldu. 1884-cü ildə universitetdən məzuniyyət götürərək, Leypsiq Universitetində Feliks Klein ilə işləməyə başladı. 1927-ci ildə təqaüdə çıxana qədər, Vyanaya qayıdana qədər Praqada qaldı. Pik 1911-ci ildə Albert Eynşteyni riyazi fizika professoru təyin edən (o vaxtkı) Alman Praqa Universitetində komitəyə sədrlik edirdi. Pik Çexiya Elmlər və İncəsənət Akademiyasının üzvü seçildi, lakin nasistlərin Praqanı ələ keçirməsindən sonra ölkədən çıxarıldı. 1927-ci ildə təqaüdə çıxandan sonra Pik doğulduğu Vyanaya qayıtdı. Anşlusdan sonra nasistlər 12 mart 1938-ci ildə Avstriyaya daxil olduqdan sonra Piek Praqaya qayıtdı. 1939-cu ilin martında faşistlər Çexoslovakiyaya hücum etdilər. George göndərildi konsentrasiya düşərgəsi Theresienstadt 13 iyul 1942. O, iki həftə sonra öldü.

Pik teoremi. Pik teoremi kombinator həndəsəsinin və ədədlərin həndəsəsinin klassik nəticəsidir. Tam təpələri olan çoxbucaqlının sahəsi B + D/2 - 1 cəminə bərabərdir, burada B çoxbucaqlı daxilindəki tam nöqtələrin sayı, D isə çoxbucaqlının sərhədindəki tam nöqtələrin sayıdır.

Pik teoreminin yaltaq sübutu. İstənilən belə çoxbucaqlı asanlıqla şəbəkənin qovşaqlarında təpələri olan üçbucaqlara bölünə bilər, içərisində və ya yanlarında heç bir qovşaq yoxdur. Göstərilə bilər ki, bütün bu üçbucaqların sahələri eyni və 1/2-ə bərabərdir və buna görə də çoxbucaqlının sahəsi onların T sayının yarısına bərabərdir. Bu ədədi tapmaq üçün n ilə işarə edirik. poliqonun tərəflərinin sayı, i ilə - onun daxilindəki qovşaqların sayı və b ilə - təpələri daxil olmaqla, tərəflərdəki qovşaqların sayı. Bütün üçbucaqların bucaqlarının ümumi cəmi πТ-dir. İndi bu məbləği başqa cür tapaq. İstənilən daxili qovşaqda təpəsi olan bucaqların cəmi 2 π, yəni belə bucaqların ümumi cəmi 2 π i-dir; təpələrində deyil, tərəflərdəki düyünlərdəki bucaqların cəmi (b - n) π, çoxbucaqlının təpələrindəki bucaqların cəmi isə (n - 2) π-dir. Beləliklə, π T \u003d 2i π + (b - n) π + (n - 2) π, ondan Pik düsturu kimi tanınan çoxbucaqlının S sahəsi üçün ifadə alırıq. Məsələn, rəqəmdə b = 9, i = 24 və buna görə də çoxbucaqlının sahəsi 27,5-dir.

Ərizə. Beləliklə, B6 tapşırığına qayıdın. İndi yeni düsturla tanış olaraq bu dördbucağın sahəsini asanlıqla tapa bilərik. B 5 olduğundan; D - 14, sonra 5 + 14: 2-1 \u003d 11 (sm kvadrat) Bu dördbucağın sahəsi 11 sm kvadratdır.

Eyni düsturdan istifadə edərək üçbucağın sahəsini tapa bilərik. B-14, G-10, sonra 14+10:2-1=18 (kvadrat sm) olduğundan bu üçbucağın sahəsi 18 sm kvadratdır.

B-9, D-12 olarsa, onda: 9+12:2-1=14 (sm kvadrat) Bu dördbucağın sahəsi 14 sm kvadratdır.

Düsturun əhatə dairəsi. Düsturun müxtəlif növ imtahanlarda, tapşırıqlarda və sairdə istifadə olunması ilə yanaşı, ətrafımızdakı bütün dünyanı müşayiət edir.

Pik düsturuna görə S = B + ½ G-1 1) bədən B=9, G=26, S=9+½ 26-1=9+13-1= 21 2) quyruq B=0, G=8, S= 0 +½ 8 -1= 3 3) S= 21+3=24

Peak düsturuna görə S \u003d B + ½ G-1 B \u003d 36, G \u003d 21 S \u003d 36 + ½ 21 -1 \u003d 36 + 10,5-1 \u003d 45,5

Nəticə. Nəticədə belə qənaətə gəldim ki, məktəb kurikulumunda öyrənilməyən sahə problemlərinin həlli üçün çoxlu müxtəlif yollar var və onları Seçim düsturunun nümunəsi ilə göstərdim.

kataloq. Öz-özünə kəsişmələri olmayan çoxbucaqlı, bütün təpələri tam koordinatları olan nöqtələrdə olarsa, şəbəkəli çoxbucaqlı adlanır (Dekart koordinat sistemində). Koordinat müstəvisindəki nöqtənin hər iki koordinatı tam ədəddirsə, ona tam ədəd deyilir.