Calculating the area of a figure.
Pick method
The work of a student of class 5B MBOU secondary school No. 23 in Irkutsk
Balsukova Alexandra
Head: Khodyreva T.G.
2014
Calculating the area of a figure. Pick Method
Object of study : tasks on checkered paper
Subject of study : problems for calculating the area of a polygon on checkered paper, methods and techniques for solving them.
Research methods Keywords: comparison, generalization, analogy, study of literature and Internet resources, information analysis.
Purpose of the study:
choose the main, interesting, understandable information
Analyze and organize the information received
Find different methods and techniques for solving problems on checkered paper
check the formulas for calculating the areas of geometric shapes using the Peak formula
Create an electronic presentation of the work to present the collected material
Geometry is the most powerful tool for the refinement of our mental faculties and enables us to think and reason correctly.
(G. Galileo)
Relevance of the topic
Passion for mathematics often begins with thinking about a problem. So, when studying the topic "Areas of polygons", the question arises whether there are tasks that are different from the tasks considered in the textbook. Such tasks include tasks on checkered paper. What is the peculiarity of such problems, are there special methods and techniques for solving problems on checkered paper. In a math class, the teacher introduced us to an interesting method for calculating polygons. I began to study the literature, Internet resources on this topic. It would seem that fascinating things can be found on a checkered plane, that is, on an endless piece of paper, lined into identical squares. It turns out that the tasks associated with checkered paper are quite diverse. I learned how to calculate the areas of polygons drawn on a checkered piece of paper. For many tasks, there is no checkered paper general rule solutions, specific methods and techniques. This is their property that determines their value for the development of not a specific educational skill or skill, but in general the ability to think, reflect, analyze, look for analogies, that is, these tasks develop thinking skills in their broadest sense.
And I also learned that such tasks are considered in the control and measuring materials of the GIA and the Unified State Examination. Therefore, I consider the study of this material useful for its application not only in the future educational process, but also for solving non-standard Olympiad problems.
2.The concept of area
Square- numerical characteristic of the two-dimensional geometric figure, showing the size of this shape. Historically, area calculation was called . A figure that has area is called squaring .
The area of a flat figure in terms of geometry
1. Square- the measure of a flat figure in relation to the standard figure, which is a square with a side equal to one length.
2. Square- a numerical characteristic attributed to flat figures of a certain class (for example, polygons). The area of a square with a side equal to a unit of length, taken equal to a unit of area
3. Square- a positive value, the numerical value of which has the following properties:
Equal figures have equal areas;
If a figure is divided into parts that are simple figures (that is, those that can be divided into a finite number of flat triangles), then the area of \u200b\u200bthis figure is equal to the sum of the areas of its parts;
The area of a square with a side equal to the unit of measurement is equal to one.
Thus, we can conclude that the area is not a specific value, but only gives some conditional characteristic of a flat figure. To find the area of an arbitrary figure, it is necessary to determine how many squares with a side equal to one length, it contains. For example, let's take a rectangle in which a square centimeter fits exactly 6 times. This means that the area of the rectangle is 6 cm2.
The choice of the area of a square with a side equal to the unit of measurement as the minimum unit of measurement for all areas is not accidental. This is the result of an agreement between people that arose in the course of "natural" centuries-old selection. In addition, there were other proposals for a unit of measure. So, for example, it was proposed to take the area of an equilateral triangle as such a unit (i.e., any flat figure could be represented as a “sum” of a certain number equilateral triangles), which would lead to a change in the numerical representation of areas.
Thus, formulas for calculating areas appeared in mathematics and were not immediately realized by a person - this many scientists living in different eras and different countries. (Wrong formulas did not find a place in science and went into oblivion). The true formulas were supplemented, corrected and substantiated over thousands of years, until they reached us in their modern form.
Of course area measurement consists in comparing the area of a given figure with the area of a figure taken as a unit of measurement. As a result of the comparison, a certain number is obtained - the numerical value of the area of \u200b\u200bthe given figure. This number shows how many times the area of a given figure is greater (or less) than the area of the figure, taken as a unit of area.
T 
Thus, we can conclude that the area is an artificial quantity, historically introduced by man to measure some property of a flat figure. The need to enter such a value was due to the growing need to know how large this or that territory is, how much grain is needed to sow a field or calculate the floor surface area for decorating ornamental tiles.
Peak Formula
To estimate the area of a polygon on checkered paper, it is enough to calculate how many cells this polygon covers (we take the area of \u200b\u200bthe cell as a unit). More precisely, ifS is the area of the polygon, B is the number of cells that lie entirely inside the polygon, and G is the number of cells that have an interior. We will consider only such polygons, all the vertices of which lie at the nodes of the checkered paper - in those where the grid lines of the polygon intersect at least one common point.
The area of any triangle drawn on checkered paper can be easily calculated by representing it as the sum or difference of the areas of right-angled triangles and rectangles whose sides follow the grid lines passing through the vertices of the drawn triangle.
To calculate the area of such a polygon, you can use the following theorem:
Theorem . Let - the number of integer points inside the polygon, - the number of integer points on its boundary, - its area. ThenPick's formula:
Example. For the polygon in the figureL = 7 (red dots), 9 (green dots), soS = 7+ 9/2 -1 = 10,5 square units.
Pick's theorem- classic result and .
The area of a triangle with vertices at the nodes and containing no nodes either inside or on the sides (except for the vertices) is equal to 1/2. This fact.
3. History
Pick's formula was discovered by the Austrian mathematician Georg Alexander (1859-1942) in . At the age of 16, Georg finished school and entered. At the age of 20 he received the right to teach physics and mathematics. In 1884 Peak went to to . There he met another student of Klein,. Later, in 1885, he returned towhere he spent the rest of his scientific career.
Georg Pick was friends with Einstein. Pick and Einstein not only shared scientific interests, but were also passionate about music. Pick, who played in a quartet that consisted of university professors, introduced Einstein to the scientific and musical societies of Prague.
The circle of mathematical interests of Peak was extremely wide. In particular, they are more than 50 scientific works. Pick's theorem, discovered by him in 1899, was widely known for calculating the area of a polygon. In Germany, this theorem is included in school textbooks.
4.Applications of Pick's Formula
The Pick formula is used not only to calculate the areas of polygons, but also to solve many problems of the Olympiad level.
Some examples of using Pick's formula when solving problems:
1) The chess king went around the board of 8 × 8 cells, having visited each
home field exactly once and with the last move returning to the original
field. A broken line connecting in series the centers of the fields that
the king passed, has no self-intersections. What area can
limit this broken line? (The side of the cell is 1.)
It immediately follows from the Pick formula that the area bounded by the lo-
mana is 64/2 − 1 = 31; here the lattice nodes are the centers 64
fields and, by assumption, they all lie on the boundary of the polygon. So
Thus, although there are quite a lot of such "trajectories" of the king, but all of them
limit polygons of equal areas.
Tasks from the control and measuring materials of the GIA and the Unified State Examination
Task B3
Find the area of the figure depicted on checkered paper with a cell size of 1 cm 1 cm (see Fig.). Give your answer in square centimeters.
4.Conclusion
In the process of research, I studied reference, popular science literature. I learned that the problem of finding the area of a polygon with vertices at the nodes of the grid inspired the Austrian mathematician Pick in 1899 to prove the wonderful Pick formula.
As a result of my work, I expanded my knowledge of solving problems on checkered paper, determined for myself the classification of the problems under study, and became convinced of their diversity.
I learned how to calculate the areas of polygons drawn on a checkered sheet. The considered tasks have a different level of difficulty - from simple to Olympiad. Everyone can find among them tasks of a feasible level of complexity, starting from which, it will be possible to move on to solving more difficult ones.
I came to the conclusion that the topic that interested me is quite multifaceted, the tasks on checkered paper are diverse, the methods and techniques for solving them are also diverse. Therefore, our I decided to continue working in this direction.
5. Literature used:
1. N. B. Vasil’ev, “Around the Pick formula,” Kvant. - 1974. - No. 12
2. Kokse Prasolov VV Tasks in planimetry. - M.: MTsNMO, 2006.t e r G.S.M. Introduction to geometry. - M.: Nauka, 1966
3. Roslova L.O., Sharygin I.F. Measurements. - M.: Ed. "Open World", 2005.
Internet resources:
:
Feedback on work
"Calculation of areas flat figures. Pick Method"
Consideration of this topic will improve cognitive activity a student who later on in geometry lessons will begin to see the harmony of the drawing and will cease to perceive geometry (and mathematics in general) as a boring science.
Reviewed by math teacher
Khodyreva Tatyana Georgievna
Peak Formula
1. Introduction
2. Peak formula. Proof I.
Proof II.
The proof of Sh.
3. Tasks.
4. The formula for the area of a polygon in terms of the coordinates of the vertices.
5. Tasks.
6. Literature
Peak formula.
1. Introduction.
We draw wisdom from history,
in poetry - wit,
in mathematics - insight.
F. Bacon
The plot will unfold on a regular piece of checkered paper.
The lines going along the sides of the cells form a grid, and the vertices of the cells are the nodes of this grid. Let's draw a polygon on the sheet with vertices at the nodes and find its area.
You can search for it in different ways. For example, you can cut a polygon into fairly simple shapes, find their areas and add them up.
But here we are in for a lot of trouble. The figure is easily broken into rectangles, trapezoids, and triangles, and its area is calculated effortlessly.
Although the polygon looks simple enough, it will take a lot of work to calculate its area. What if the polygon looked fancier? It turns out that the areas of polygons whose vertices are located at the nodes of the grid can be calculated much more simply: there is a formula that relates their area to the number of nodes lying inside and on the border of the polygon. This wonderful and simple formula is called Pick's formula.
2. Peak formula.
The vertices of a polygon (not necessarily convex) are located at the nodes of an integer lattice. Inside it lies B nodes of the lattice, and on the border of G nodes. Let us prove that its area is B + 
– 1 (Peak's formula).
Proof I.
Consider a polygon whose vertices are at the nodes of an integer lattice, that is, they have integer coordinates.
We divide the polygon into triangles with vertices at the nodes of the lattice, which do not contain nodes either inside or on the sides.
Denote:
n is the number of sides of the polygon,
m is the number of triangles with vertices at the nodes of the lattice that do not contain nodes either inside or on the sides,
B is the number of nodes inside the polygon,
Г is the number of nodes on the sides, including the vertices.
The areas of all these triangles are the same and equal.
Therefore, the area of the polygon is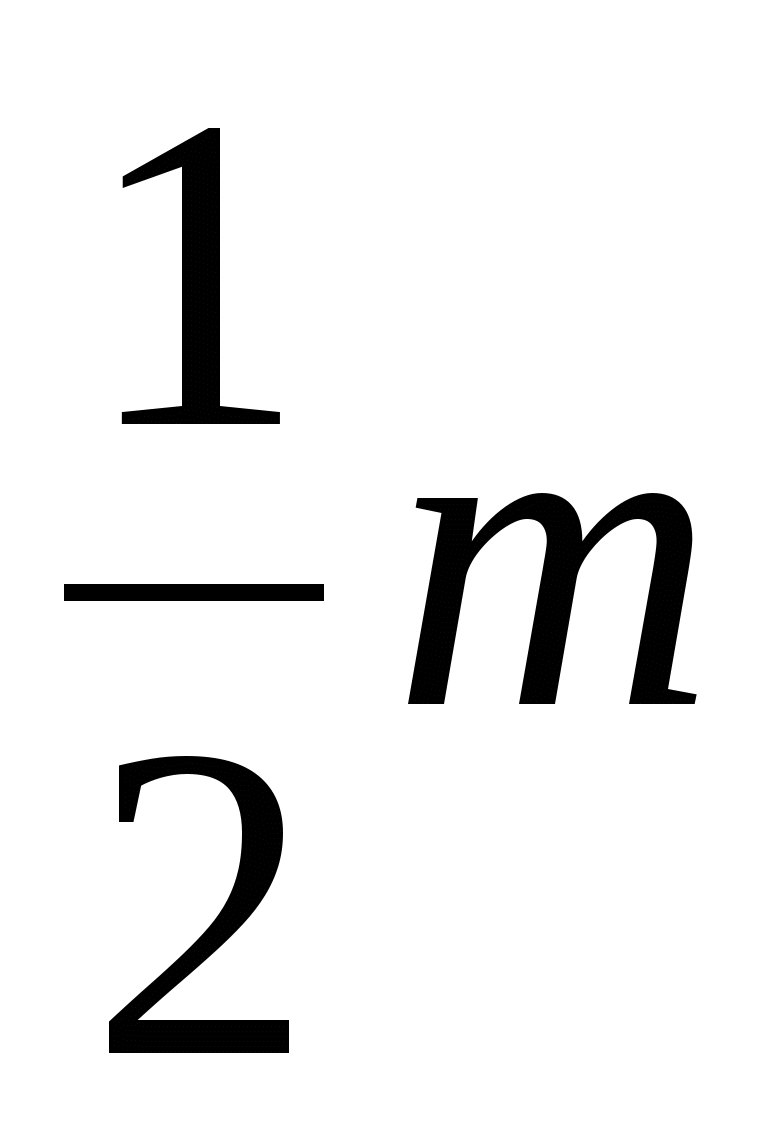 
.
180 0 m .
Now let's find this sum in a different way.
The sum of angles with a vertex at any internal node is 360 0 .
Then the sum of angles with vertices at all internal nodes is equal to 360 0 V.
The total sum of the angles at the nodes on the sides, but not at the vertices, is 180 0 (G - n).
The sum of the angles at the vertices of the polygon is 180 0 ( n – 2) .
The total sum of the angles of all triangles is 360 0 V + 180 0 (G - n) + 180 0 (n – 2).
So 180 0 m\u003d 360 0 V + 180 0 (G - n) + 180 0 (n – 2),
180 0 m\u003d 360 0 V + 180 0 G - 180 0 n + 180 0 n– 180 0 2,
180 0 m\u003d 360 0 V + 180 0 G– 360 0,
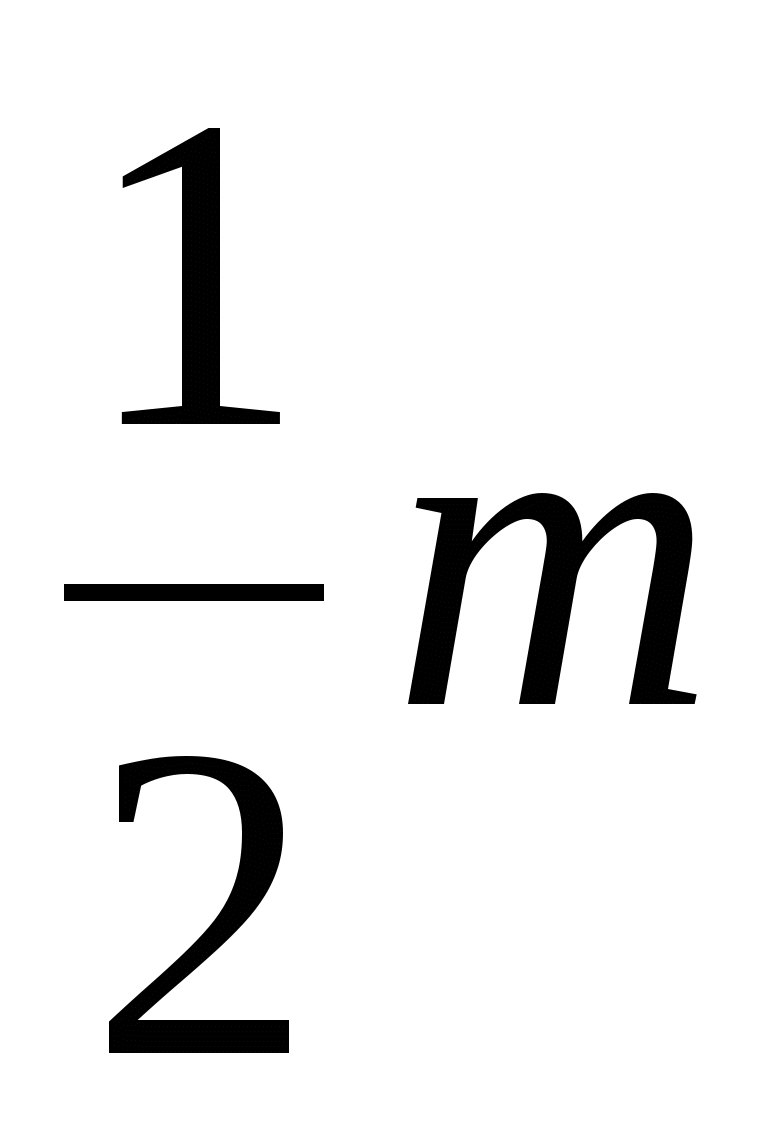= B + 
– 1 ,
whence we obtain the expression for the area S of the polygon:
S= B + – 1 ,
known as Pick's formula.
In the figure: V = 24, D = 9, therefore,S = 24 + – 1 = 27,5.
Find the area of the first polygon using the Peak formula:
B = 28 (green dots);
D = 20 (blue dots).
We get, S =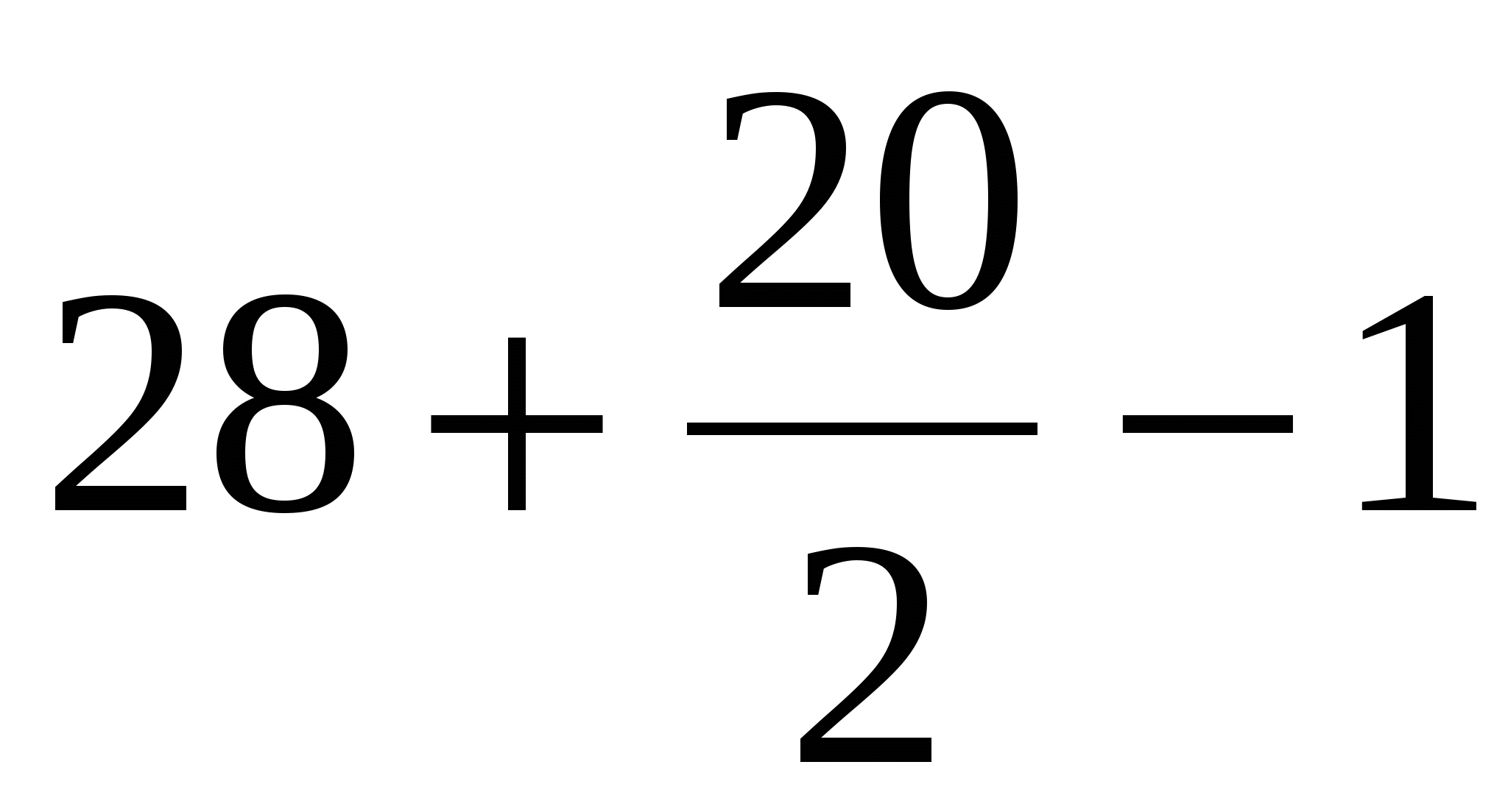 
= 37 square units
Proof II.
To each polygon M with vertices at the nodes of an integer lattice we assign the number f (M) = 
, where the summation is over all lattice nodes belonging to M, and the angle 
is defined as follows: 
= 
for an interior point of a polygon, 
= 
for a boundary point other than a vertex, and – angle at the vertex, if the given node is a vertex. It is easy to see that f (M) = 
+ 
= B + – 1. It remains to check that the number f (M) is equal to the area of the polygon M.
Let the polygon M be cut into polygons M 1 and M 2 with vertices at the nodes of the lattice. Then f(M) = f(M 1) + f(M 2), since for each node the angles add up. Therefore, if Pick's formula is true for two of the polygons M, M 1 and M 2, then it is also true for the third.
If M is a rectangle with sides p and q, directed along the lattice lines, then
f (M) = (p – 1)(q – 1) + 
= pq.
In this case, Pick's formula is valid. By cutting the rectangle M diagonally into triangles M 1 and M 2 and using the fact that f (M) = f (M 1) + f (M 2) and f (M 1) = f (M 2), it is easy to prove the validity of Pick's formula for any right triangle with legs directed along the lines of the lattice. By cutting off several such triangles from a rectangle, any triangle can be obtained.
To complete the proof of Pick's formula, it remains to note that any polygon can be cut into triangles by non-intersecting diagonals.
The proof of Sh.
The connection between the area of a figure and the number of nodes that fall into this figure is especially clear in the case of a rectangle.
Let ABCD- a rectangle with vertices at the nodes and sides going along the grid lines.
Denote by AT the number of nodes lying inside the rectangle, and through G is the number of nodes on its boundary. Move the grid half a cell to the right and half a cell down.
Then the territory of the rectangle can be "distributed" between the nodes as follows: each of AT nodes "controls" the whole cell of the shifted grid, each of G- 4 boundary non-corner nodes - half of the cell, and each of the corner points - a quarter of the cell. Therefore, the area of the rectangle S is
So, for rectangles with vertices at nodes and sides going along grid lines, we have established the formula 
Let us prove that this formula is true not only for rectangles, but also for arbitrary polygons with vertices at the grid nodes.
Denote by S
m
polygon areaM
with vertices at nodes, and throughP
m
- value 
, whereAT
m
is the number of nodes insideM, a G
m
is the number of nodes on the boundary. Then the Pick formula can be written as 
.
We divide the proof of the formula into several steps.
Step 1.
If polygonM
with vertices at grid nodes cut into 2 polygonsM
1
and M
2
,
also having vertices only at the grid nodes, then 
. Let the polygonM
cut into polygonsM
1
and M
2
with vertices at nodes by a segment AB. All nodes, except those that fall on the segmentAB,
give the same contribution to the left and right parts of the formula. Consider the nodes lying on the segment AB.
If such a node lies between A and B (for example, C), then for a polygonM
it is internal, and for polygonsM
1
and M
2
- boundary. Therefore, his contribution toP
m
equals 1, and in each of the expressions 
and 
– 0.5 each, that is, the contributions of such a node toP
m
and 
are equal.
Consider nodes A and B. They are boundary both for M, and for M 1 , M 2 .
Therefore, the contribution of each of these nodes toP
m
is 0.5 a -
unit. This means that the total contribution of nodes A and B toP
m
equals 1, which is 1 less than their contribution to .
But 
, a .
From the total "contribution" of all nodes P m 1 is subtracted from 2 is subtracted, and this compensates for the difference in the contributions of nodes A and B.
So, .
Step 2
If polygon M with vertices at the grid nodes cut into two polygons M 1 and M 2 (also with vertices at nodes) and the formula is true for some two of the polygons MM 1 , M 2 , then it is also true for the third polygon.
Let, for example, it is true forM
1
and M
2
,
that is 
. Then (on the first step),
but on
first step), the last expression is equal toP
m
,
and equality 
and there is the Pick formula.
Step 3
Let us prove Pick's formula for a right triangle with vertices at the grid nodes and legs lying on the grid lines.
Triangle ABC build to a rectangle ABCD .
For rectangles, Pick's formula is correct: S ABCD = P ABCD . According to the first step P ABCD = P ABC + P ACD , P ABC = P ACD , so P ABCD = 2P ABC . But S ABCD = 2 S ABC . That's why S ABC = P ABC .
Step 4
Pick's formula is correct for an arbitrary triangle with vertices at the grid nodes.
Having examined the figure, it is easy to understand: any such triangle can be obtained by “cutting off” from some rectangle with sides running along the grid lines, several rectangles and right-angled triangles with legs on the grid lines. And since Pick's formula is true for rectangles and right-angled triangles, then (remember step 2) it is also true for the original triangle.
We have proved that if a polygon can be cut into triangles with vertices at the nodes of the grid, then Pick's formula is true for it.
3. Tasks.
Find the area of the figures:
1
.
B=9
G = 4
B=9
G = 5
The text of the work is placed without images and formulas.
Full version work is available in the "Files of work" tab in PDF format
Introduction
I am a 6th grade student. I started studying geometry since last year, because I study at school using the textbook “Mathematics. Arithmetic. Geometry” edited by E.A. Bunimovich, L.V. Kuznetsova, S.S. Minaeva and others.
My greatest attention was attracted by the topics "Squares of figures", "Compilation of formulas". I noticed that the areas of the same figures can be found in different ways. In everyday life, we often face the problem of finding the area. For example, find the floor area to be painted. It is curious, after all, in order to buy the required amount of wallpaper for renovation, you need to know the size of the room, i.e. wall area. Calculating the area of a square, a rectangle and a right-angled triangle did not cause me any difficulties.
Intrigued by this topic, I began to look for additional material on the Internet. As a result of searching, I came across the Pick formula - this is a formula for calculating the area of \u200b\u200ba polygon drawn on checkered paper. Calculating the area using this formula seemed to me accessible to any student. That is why I decided to research work.
Relevance of the topic:
This topic is an addition and deepening of the study of the geometry course.
Studying this topic will help you better prepare for olympiads and exams.
Objective:
Familiarize yourself with the Pick formula.
Master decision making geometric problems using Pick's formula.
Systematize and generalize theoretical and practical materials.
Research objectives:
Check the effectiveness and expediency of applying the formula in solving problems.
Learn how to apply the Pick formula to problems of varying complexity.
Compare problems solved using the Pick formula and the traditional way.
Main part
1.1. History reference
Georg Alexander Pick is an Austrian mathematician born August 10, 1859. He was gifted child, he was taught by his father, who headed a private institute. At 16, Georg graduated from high school and entered the University of Vienna. At the age of 20 he received the right to teach physics and mathematics. The formula for determining the area of a lattice of polygons brought him worldwide fame. He published his formula in an article in 1899. It became popular when the Polish scientist Hugo Steinhaus included it in 1969 in a publication of mathematical pictures.
Georg Pieck was educated at the University of Vienna and completed his PhD in 1880. After receiving his doctorate, he was appointed assistant to Ernest Mach at the Scherl-Ferdinand University in Prague. There he became a teacher. He remained in Prague until his retirement in 1927 and then returned to Vienna.
Pick chaired the committee at the German University of Prague that appointed Einstein professor of mathematical physics in 1911.
He was elected a member of the Czech Academy of Sciences and Arts, but was expelled after the Nazi takeover of Prague.
When the Nazis entered Austria on March 12, 1938, he returned to Prague. In March 1939, the Nazis invaded Czechoslovakia. On July 13, 1942, Pick was deported to the Theresienstadt camp set up by the Nazis in northern Bohemia, where he died two weeks later at the age of 82.
1.2. Research and proof
I began my research work by asking the question: What areas of figures can I find? I could make a formula for calculating the area of various triangles and quadrilaterals. But what about five-, six-, and in general with polygons?
In the course of research on various sites, I saw solutions to problems for calculating the area of \u200b\u200bfive-, six-, and other polygons. The formula for solving these problems was called Pick's formula. She looks like this :S =B+G/2-1, where AT- the number of nodes lying inside the polygon, G- the number of nodes lying on the border of the polygon. The peculiarity of this formula is that it can only be applied to polygons drawn on checkered paper.
Any such polygon can be easily divided into triangles with vertices at the nodes of the lattice, containing no nodes either inside or on the sides. It can be shown that the areas of all these triangles are the same and equal to ½, and therefore the area of the polygon is equal to half their number T.
To find this number, we denote by n the number of sides of the polygon, by AT- the number of nodes inside it, through G is the number of nodes on the sides, including the vertices. The total sum of the angles of all triangles is 180°. T.
Now let's find the sum in a different way.
The sum of angles with a vertex at any internal node is 2.180°, i.e. the total sum of the angles is 360°. AT; the total sum of the angles at the nodes on the sides but not at the vertices is ( Mr. n)180°, and the sum of the angles at the vertices of the polygon will be equal to ( G- 2)180°. In this way, T= 2.180°. B+(G-n)180°+(n -2)180 °. By expanding the brackets and dividing by 360°, we get the formula for the area S of a polygon, known as Pick's formula.
2. Practical part
I decided to check this formula on tasks from the OGE-2017 collection. I took tasks to calculate the area of a triangle, a quadrilateral and a pentagon. I decided to compare the answers, solving in two ways: 1) I added the figures to a rectangle and subtracted the area of right-angled triangles from the area of the resulting rectangle; 2) applied the Peak formula.
S = 18-1.5-4.5 = 12 and S = 7+12/2-1= 12
S = 24-9-3 = 12 and S = 7+12/2-1 = 12
S = 77-7.5-12-4.5-4 = 49 and S = 43+14/2-1 = 49
Comparing the results, I conclude that both formulas give the same answer. Finding the area of a figure using the Peak formula turned out to be faster and easier, because there were fewer calculations. The ease of decision and saving time on calculations will be useful to me in the future when passing the OGE.
This prompted me to test the possibility of applying the Pick formula to more complex figures.
S = 0 + 4/2 -1 = 1
S \u003d 5 + 11 / 2-1 \u003d 9.5
S=4+16/2-1=1
Conclusion
Pick's formula is easy to understand and easy to use. First, it is enough to be able to count, divide by 2, add and subtract. Secondly, you can find the area and a complex figure without spending a lot of time. Thirdly, this formula works for any polygon.
The disadvantage is that the Pick Formula is applicable only for figures that are drawn on checkered paper and the vertices lie on the nodes of the cells.
I am sure that when passing final exams, problems for calculating the area of \u200b\u200bfigures will not cause difficulties. After all, I am already familiar with the Pick formula.
Bibliography
Bunimovich E.A., Dorofeev G.V., Suvorova S.B. etc. Mathematics. Arithmetic. Geometry. Grade 5: textbook. for general education organizations with app. to an electron. carrier -3rd ed.-M.: Enlightenment, 2014.- 223, p. : ill. - (Spheres).
Bunimovich E.A., Kuznetsova L.V., Minaeva S.S. etc. Mathematics. Arithmetic. Geometry. Grade 6: textbook. for general education organizations-5th ed.-M.: Education, 2016.-240s. : ill.- (Spheres).
Vasiliev N.B. Around the Pick formula. //Quantum.- 1974.-№2. -p.39-43
Rassolov V.V. Problems in planimetry. / 5th ed., corrected. And extra. - M.: 2006.-640s.
I.V. Yaschenko. OGE. Mathematics: typical exam options: O-39 36 options - M .: National Education Publishing House, 2017. -240 p. - (OGE. FIPI-school).
"I will solve the OGE": mathematics. The training system of Dmitry Gushchin. OGE-2017: tasks, answers, solutions [Electronic resource]. Access mode: https://oge.sdamgia.ru/test?id=6846966 (Accessed 04/02/2017)
To estimate the area of a polygon on checkered paper, it is enough to calculate how many cells this polygon covers (we take the area of \u200b\u200bthe cell as a unit). More precisely, if S is the area of the polygon, is the number of cells that lie entirely inside the polygon, and is the number of cells that have at least one common point with the interior of the polygon.
We will consider below only such polygons, all of whose vertices lie in the nodes of the checkered paper - in those where the grid lines intersect. It turns out that for such polygons, you can specify the following formula:
where is the area, r is the number of nodes that lie strictly inside the polygon.
This formula is called the “Peak formula” after the mathematician who discovered it in 1899.
simple triangles
The area of any triangle drawn on checkered paper can be easily calculated by representing it as the sum or difference of the areas of right-angled triangles and rectangles whose sides follow the grid lines passing through the vertices of the drawn triangle. Having done this, for example, for the triangles shown in Figure 1.34, you can make sure that the area is always equal to the "received" number - the number of the form, where is an integer.
Let's call a triangle simple if there are no grid nodes either inside it or on its sides, except for the vertices. All simple triangles in Fig. 1.34 have an area. We will see that this is no accident.
A task. Three grasshoppers (three points) at the initial moment of time sit at three vertices of one cell, and then begin to “play leapfrog”: each can jump over one of the other two, after which it ends up in a point symmetrical with respect to it (Fig. 1.35, clearly, that after any number of such jumps, the grasshoppers will fall into knots of checkered paper). In what triples of points can grasshoppers end up after several jumps?
We call a triangle reachable if three grasshoppers can simultaneously appear at its vertices, which were initially at three vertices of the same cell; we will call a jump a transformation of a triangle, which consists in the fact that one of the vertices goes to a point that is symmetrical with respect to any of the other two vertices (these two vertices remain in place).
Theorem 1. The following three properties of triangles with checkered paper knots are equivalent to each other:
1) the triangle has an area,
2) the triangle is simple,
3) the triangle is reachable.
Let's get acquainted with the following properties of a simple triangle, which lead to the validity of this theorem.
1. The area of a triangle does not change when jumping.
2. Any reachable triangle has an area.
3. If you complete a simple triangle ABC to parallelogram ABCD, then there will be no nodes either inside or on the sides of this parallelogram (not counting the vertices).
4. From a simple triangle, when jumping, you get a simple one.
5. From a simple triangle, one of the angles is obtuse or right (moreover, the latter case is possible only for a triangle whose three vertices belong to the same cell, we will call such a simple triangle with sides 1, 1 minimal.)
6. From any simple non-minimal triangle, one jump can get a triangle whose largest side is less than the largest side of the original one.
7. Any simple triangle can be converted into a minimal one by a finite number of jumps.
8. Any simple triangle is reachable.
9. Any simple triangle has an area.
10. Any triangle can be cut into simple ones.
11. The area of any triangle is equal, and for any cutting it into simple ones, their number is m.
12. Any area triangle is simple.
13. For any two nodes BUT and AT lattices on the segment between which there are no other nodes, there is a node FROM such that the triangle ABC- simple.
14. Knot FROM in the previous property, you can always choose so that the angle DIA be blunt or straight.
15. Let the checkered plane be cut into equal parallelograms so that all nodes are vertices of parallelograms. Then each of the triangles into which one of these parallelograms is cut by its diagonal is simple.
16. (Reverse 15). Triangle ABC is simple if and only if all possible triangles obtained from ABC parallel transfers that transfer the node BUT to different nodes of the lattice, do not overlap.
17. If the lattice - checkered paper nodes - is divided into four sublattices with cells (Fig. 1.36), then the vertices of a simple triangle will necessarily fall into three different sublattices (all three have different designations).
The next two properties give the answer to the three grasshopper problem.
18. Three grasshoppers can simultaneously hit those and only those triples of points that serve as vertices of a simple triangle and have the same sign as the corresponding vertices of the initial triangle.
19. Two grasshoppers can simultaneously hit those and only those pairs of nodes of the corresponding signs, on the segment between which there are no other nodes.
Polygon triangulation
We will consider a particular form of polygons on checkered paper, to which the values \u200b\u200bare corresponding in the Pick formula. But from this particular case, you can go straight to the most general one, using the theorem on cutting an arbitrary polygon into triangles (checkered paper is no longer needed).
Let some polygon and some finite set be given on the plane To points lying inside the polygon and on its boundary (moreover, all the vertices of the polygon belong to the set To).
Triangulation with vertices To is called a partition of a given polygon into triangles with vertices in the set To such that each point in To serves as a vertex for each of those triangulation triangles to which this point belongs (that is, points from To do not fall inside or on the sides of the triangles, fig. 1.37).
Theorem 2. a) Any n-gon can be cut by diagonals into triangles, and the number of triangles will be equal to n- 2 (this partition is a triangulation with vertices in vertices n-gon).
b) Let r points (including all vertices), inside - more i points. Then there is a triangulation with vertices at marked points, and the number of triangles of such a triangulation will be equal.
Of course, a) is a special case of b), when.
The validity of this theorem follows from the following assertions.
1) From the top of the largest angle n-gon () you can always draw a diagonal that lies entirely inside the polygon.
2) If n-gon cut diagonally into R-gon and q-gon, then.
3) Sum of angles n-gon is equal.
4) Any n-gon can be cut diagonally into triangles.
5) For any triangle, inside and on the boundary of which several points are marked (including all three of its vertices), there is a triangulation with vertices at the marked points.
6) The same is true for any n-gon.
7) The number of triangulation triangles is, where i and r- the number of marked points respectively inside and on the border of the polygon. Let's call the partition n-gon into several polygons is correct if each vertex of one of the partition polygons serves as a vertex of all other partition polygons to which it belongs. 8) If from vertices k-gons into which it is divided in the right way n-gon, i vertices lie inside and r- on the border n-gon, then the number k-gons equals
9) If the points of the plane and the segments with ends at these points form a polygon, correctly divided into polygons, then (Fig. 1.38)
It is from Theorems 1 and 2 that the Pick formula follows:
1.5 The Pythagorean theorem on the sum of the areas of squares built on the legs of a right triangle
Theorem. The sum of the areas of the squares built on the legs of a right triangle is equal to the area of the square built on the hypotenuse of this triangle. Proof. Let ABC(Fig. 1.39) is a right triangle, and BDEA, AFGE and BCKH- squares built on its legs and hypotenuse; it is required to prove that the sum of the areas of the first two squares is equal to the area of the third square.
Let's spend sun. Then square BCKH split into two rectangles. Let us prove that the rectangle BLMH equal to a square BDEA, and the rectangle LCKM equal to a square AFGC.
Draw auxiliary lines DC and AN. Consider triangles DCB and ABH. Triangle DCB having a basis BD, common with square BDEA, and the height CN, equal to the height AB this square is equal to half the square. Triangle AVN having a basis VN, common with a rectangle BLMH, and height AR, equal to the height BL of this rectangle is equal to half of it. Comparing these two triangles with each other, we find that they have BD = VA and BC = HH(like the sides of a square);
More than that, DCB= AVN, because each of these angles consists of a common part - ABC and right angle. So the triangles AVN and BCD are equal. It follows that the rectangle BLMN equal to a square BDEA. In the same way, it is proved that the rectangle LGKM equal to a square AFGC. It follows that the square FAPC equal to the sum of squares BDEA and AFGC.
To use the preview of presentations, create a Google account (account) and sign in: https://accounts.google.com
Slides captions:
Completed by a student of secondary school No. 7 8 "A" class Yunosheva Ksenia Instructor: Babina Natalya Alekseevna Salsk 2011 "Peak Formula"
Objectives of the work: Finding out the existence of another, different from the school curriculum, formula for finding the area of a lattice polygon. Areas of application of the desired formula.
Introduction. Mathematics education received in general education schools, is the most important component general education and general culture modern man. At this stage, school system designed for eleven years of study. All students at the end of the eleventh grade will have to take the Unified State Exam, which will show the level of knowledge gained while studying at school. But the school curriculum does not always provide the most rational ways to solve any problems. For example, looking at USE results 2010 shows that many students lose points due to task B6. I set out to figure out how to save time and solve this problem correctly.
Task B6. Figures are depicted on checkered paper with cells measuring 1 cm by 1 cm (see figure). Find their area in square centimeters.
So, in order to still solve this task, I need to apply the formulas for finding the area, which we study in grade 8. But it will take a lot of time, and I need to answer the question as quickly as possible, because the time for the exam is strictly limited. Therefore, after doing research, I found out that there is Pick's theorem, which is not studied in the school curriculum, but which will help me cope with the task faster.
History reference. Georg Alexander Pick (August 10, 1859 – July 26, 1942) was an Austrian mathematician. He died in the Terezin concentration camp. It is known today because of Pick's formula for determining the area of a lattice of polygons. He published his formula in a paper in 1899, it became popular when Hugo Steinhaus included it in a 1969 edition of Mathematical Pictures. Pick studied at the University of Vienna and completed his PhD in 1880. After receiving his doctorate, he was appointed assistant to Ernest Mach at the Scherl-Ferdinand University in Prague. He became a teacher there in 1881. Taking a leave of absence from the university in 1884, he began working with Felix Klein at the University of Leipzig. He remained in Prague until his retirement in 1927, when he returned to Vienna. Pick chaired the committee at the (then) German University of Prague that appointed Albert Einstein professor of mathematical physics in 1911. Pick was elected a member of the Czech Academy of Sciences and Arts, but was expelled after the Nazi takeover of Prague. After retiring in 1927, Pick returned to Vienna, the city where he was born. After the Anschluss, when the Nazis entered Austria on March 12, 1938, Pieck returned to Prague. In March 1939, the Nazis invaded Czechoslovakia. George was sent to concentration camp Theresienstadt July 13, 1942. He died two weeks later.
Pick's theorem. Pick's theorem is a classical result of combinatorial geometry and the geometry of numbers. The area of a polygon with integer vertices is equal to the sum B + D/2 - 1, where B is the number of integer points inside the polygon, and D is the number of integer points on the boundary of the polygon.
A flattering proof of Pick's theorem. Any such polygon can be easily divided into triangles with vertices at the nodes of the lattice, containing no nodes either inside or on the sides. It can be shown that the areas of all these triangles are the same and equal to 1/2, and, therefore, the area of the polygon is equal to half of their number T. To find this number, we denote by n the number of sides of the polygon, by i - the number of nodes inside it and by b - the number of nodes on the sides, including the vertices. The total sum of the angles of all triangles is πТ. Now let's find this sum in a different way. The sum of angles with a vertex at any internal node is 2 π , i.e. the total sum of such angles is 2 π i ; the total sum of the angles at the nodes on the sides, but not at the vertices, is (b - n) π, and the sum of the angles at the vertices of the polygon is (n - 2) π. Thus, π T \u003d 2i π + (b - n) π + (n - 2) π, from which we obtain an expression for the area S of a polygon, known as Pick's formula. For example, in the figure b = 9, i = 24, and therefore the area of the polygon is 27.5.
Application. So, back to task B6. Now, knowing the new formula, we can easily find the area of this quadrilateral. Since B is 5; D - 14, then 5 + 14: 2-1 \u003d 11 (cm squared) The area of \u200b\u200bthis quadrangle is 11 cm squared.
Using the same formula, we can find the area of a triangle. Since B-14, G-10, then 14+10:2-1=18 (square cm) The area of this triangle is 18 cm squared.
If B-9, D-12, then: 9+12:2-1=14 (cm squared) The area of this quadrilateral is 14 cm squared.
Scope of the formula. In addition to the fact that the formula is used in various kinds of exams, assignments, and so on, it accompanies the whole world around us.
According to Peak's formula S = B + ½ G-1 1) body B=9, G=26, S=9+½ 26-1=9+13-1= 21 2) tail B=0, G=8, S= 0 +½ 8 -1= 3 3) S= 21+3=24
According to Peak's formula S \u003d B + ½ G-1 B \u003d 36, G \u003d 21 S \u003d 36 + ½ 21 -1 \u003d 36 + 10.5-1 \u003d 45.5
Conclusion. As a result, I came to the conclusion that there are many different ways to solve area problems that are not studied in the school curriculum, and showed them using the Pick formula as an example.
Directory. A polygon without self-intersections is called a lattice polygon if all its vertices are at points with integer coordinates (in the Cartesian coordinate system). A point in the coordinate plane is called integer if both of its coordinates are integers.