Harmonik xəttiləşdirmə üsulu. Qeyri-xəttilərin harmonik xəttiləşdirilməsi Harmonik xəttiləşdirmə üsulu ilə qeyri-xətti sistemin təhlili

ev » ekosistemlər Harmonik xəttiləşdirmə üsulu. Qeyri-xəttilərin harmonik xəttiləşdirilməsi Harmonik xəttiləşdirmə üsulu ilə qeyri-xətti sistemin təhlili

Bu fəsildə nəzəri cəhətdən ekvivalent xəttiləşdirmə metoduna və ya harmonik tarazlıq metoduna yaxın olan istənilən nizamlı qeyri-xətti sistemlərin sabitliyinin dövri həllərin (öz-özünə salınımların) təxmini təyini üçün harmonik xəttiləşdirmə metodu təqdim olunacaq. N.M.Krılov və N.N.Boqolyubov və nəticələrə görə - həm də BV Bulqakovun kiçik parametri üsuluna.

Nəzərdən keçirilən təxmini metod qeyri-xətti avtomatik sistemlərin sadəliyi və müxtəlif qeyri-xəttiliklərə tətbiq edildiyi zaman aparatının olduqca böyük universallığı mənasında öyrənilməsi üçün güclü vasitədir. Bununla belə, problemi təxminən həll etdiyini nəzərə almaq lazımdır. Onun tətbiqi üçün müəyyən məhdudiyyətlər var, bunlar aşağıda müzakirə olunacaq. Bu məhdudiyyətlər adətən avtomatik idarəetmə nəzəriyyəsi problemlərində yaxşı müşahidə olunur. Praktiki hesablamalar və təcrübələr bu metodun qeyri-xətti sistemlərin bir çox növləri üçün məqbul olduğunu göstərir.

Formanın bəzi qeyri-xətti ifadəsi olsun

(18.1) ifadəsinin sağ tərəfindəki funksiyanı Furye sırasına genişləndirərək, əldə edirik

bu o deməkdir ki, bu genişlənmədə daimi komponent yoxdur. Bu fəsildə biz hər yerdə sabit komponentin (18.5) olmaması şərtinin təmin olunduğunu fərz edəcəyik. Sonradan (Fəsil 19) sabit komponentin mövcudluğunda, yəni şərtin (18.5) yerinə yetirilməməsi halında, öz-özünə salınmaların öyrənilməsi metodu veriləcəkdir.

Nəzərə alsaq ki, (18.2) və (18.3)

onda (18.5) şərti ilə düstur (18.4) kimi yazıla bilər

burada q - düsturlarla təyin olunan harmonik xəttiləşdirmə əmsalları:

Beləliklə, qeyri-xətti ifadə (18.1) at ifadəsi (18.6) ilə əvəz olunur, daha yüksək harmoniklərə qədər xətti ilə oxşardır. Bu əməliyyat harmonik xəttiləşdirmə adlanır. Əmsallar sabit qiymətlərdə sabitdir, yəni dövri proses vəziyyətində. Keçici salınım prosesində a və co-nun dəyişməsi ilə q və əmsalları dəyişir (bax. Fəsil 20). Dövri proseslərin müxtəlif amplitudaları və tezlikləri üçün ifadə əmsalları (18.6) böyüklük baxımından fərqli olacaqdır. Sonrakılar üçün çox vacib olan bu vəziyyət harmonik xəttiləşdirmə ilə kitabın əvvəlki bölmələrində istifadə olunan sırf xətti ifadələrə gətirib çıxaran adi xəttiləşdirmə metodu (§ 3.1) arasında əhəmiyyətli fərqdir. Göstərilən vəziyyət, (18.6) ifadəsinə xətti tədqiqat metodlarını tətbiq etməklə, adi xəttiləşdirmə ilə aşkar edilə bilməyən qeyri-xətti sistemlərin əsas xüsusiyyətlərini təhlil etməyə imkan verəcəkdir.

Daha sadə qeyri-xəttilik üçün harmonik xəttiləşdirmə düsturlarını da veririk:

Burada iki variant mümkündür: 1) əyrinin histerezis döngəsi var (məsələn, Şəkil 16.18, c, Şəkil 16.22, d, e) və 2) əyrinin histerezis dövrəsi yoxdur (şəkil 16.8, b). , Şəkil 16.22, a və s.).

Histerezis döngəsi olduqda, törəmənin işarəsindən asılılıq faktiki müşahidə edildikdə, harmonik xəttiləşdirmədən sonra qeyri-xətti funksiya aşağıdakı ifadə ilə əvəz olunur (üçün

daimi komponent olmadıqda:

Əgər əyridə histerezis döngəsi yoxdursa, o zaman iradəsi ilə

(bir histerezis döngəsi ilə bu inteqral artan və azalan əyrinin şəklindəki fərqə görə sıfır deyildi.

Nəticə etibarilə, histerezis döngəsi olmadıqda, qeyri-xətti ifadə (18.8) daha sadə ifadə ilə əvəz olunur:

yəni daha yüksək harmoniklərə qədər əyri və ya qırıq xarakteristikası düzxətli ilə əvəz olunur, onun yamacının tangensi q salınım amplitudasının ölçüsündən asılıdır. Başqa sözlə, qeyri-xətti keçid, x giriş dəyərinin salınımlarının a amplitudasından asılı olan dişli nisbəti (qazanma) ilə "xətti" ilə bənzədilir.

Histerezis dövrəsi (18.9)-a əsasən, əlavə olaraq, faza geriləməsini verən törəmə təqdim edir, çünki beləliklə, histerezis dövrəsi şəklində qeyri-xətti koordinat gecikməsi harmonik xəttiləşmə zamanı ekvivalent xətti faza gecikməsinə çevrilir.

Aparıcı döngə ilə xüsusi qeyri-xətti əlaqə yaratmaq mümkündür, bu, törəmənin tətbiqi ilə xətti faza irəliləyişinə bərabər olacaq, lakin fərqlə, faza irəliləməsinin miqdarı salınmanın ölçüsündən asılı olacaq. amplituda, xətti sistemlərdə belə deyil.

Qeyri-xətti əlaqə müxtəlif xətti və qeyri-xətti ifadələrin cəmini özündə birləşdirən mürəkkəb tənlik ilə təsvir edildiyi hallarda, qeyri-xətti şərtlərin hər biri ayrıca harmonik xəttiləşdirməyə məruz qalır. Qeyri-xəttilik məhsulu mütləq bir mürəkkəb qeyri-xətti kimi bütöv hesab olunur. Bu halda fərqli təbiətli qeyri-xətti funksiyalar baş verə bilər.

Məsələn, (16.3) tənliklərinin ikincisinin harmonik xəttiləşdirməsi zamanı funksiya ilə məşğul olmaq lazım gələcək. Bu vəziyyətdə alırıq

şərtlə

Əgər funksiya və ya funksiya qeyri-xətti əlaqənin tənliyində yeganə qeyri-xətti funksiyadırsa, harmonik ilə

xəttiləşdirmə qoyula bilər və

əvvəlki (18.6) və (18.7) düsturlarına bənzər şəkildə. Lakin bu halda, bütün hesablamalarda a-nın dəyəri koordinat x-in özü deyil, sürət salınımlarının amplitudası olacaqdır. Bundan sonra sonuncunun amplitudası olacaq

(18.10) düsturlarından istifadə edərək harmonik xəttiləşdirmə əmsallarını hesablayarkən nəzərə almaq lazımdır ki, simmetrik qeyri-xətti xüsusiyyətləri ilə inteqralı ikiqat artırmaqla inteqral əldə etmək olar, yəni.

və mənşəyinə görə simmetrik olan histerezsiz xüsusiyyətlər üçün hesablanarkən yazmaq olar.

Ən sadə qeyri-xətti əlaqələrin bəzilərinin əmsalları üçün ifadələr veririk. Sonra onlar müxtəlif konkret problemlərin həllində birbaşa istifadə oluna bilər.

Rele əlaqələrinin harmonik xəttiləşdirmə əmsalları. Düsturlardan (18.10) istifadə edərək ən tipik rele əlaqələrinin əmsallarını və tənliklərini tapaq. Şəkildəki qrafikdə təsvir olunan rele bağlantısının xüsusiyyətlərinə ümumi bir nəzər salaq. 18.1, a, burada intervalda hər hansı kəsr ədəd var

Digər növ rele əlaqələrinin tənlikləri xüsusi hallar kimi alınacaq.

Giriş dəyərinin dalğalanmaları bir amplituda malikdirsə, o zaman Şek. 18.1 və sistemdə heç bir hərəkət olmayacaq. Amplituda olarsa, relenin dəyişdirilməsi A, B, C, D nöqtələrində baş verir (Şəkil 18.1, b), burada bizdə var.

Buna görə də xassələrdən istifadə etdikdən sonra (18.10) inteqralların hər biri üç şərtə bölünür:

və birinci və üçüncüsü, şəklə görə. 18.1, a və sıfır olacaq. Buna görə də (18.10) ifadələri formasını alır

və formanın xarakteristikası ilə rele əlaqə tənliyi şək. 18.1, lakin burada və əldə edilən dəyərlərlə (18.9) formasına sahib olacaq.

Xüsusi halları nəzərdən keçirək.

Histerezis döngəsi olmayan, lakin ölü zonalı (şəkil 18.1, a) xarakteristikalı rele bağlantısı üçün yuxarıdakı düsturlardan götürək, biz əldə edirik.

Əncir kimi bir histerezis döngəsi olan bir rele xarakteristikası üçün. bizdə olduğunu fərz etsək

Nəhayət, tapdığımız fərz etsək, ideal rele keçidi üçün (Şəkil 18.1, e).

Sonuncu misalda rele xarakteristikasının harmonik linearlaşmasının mənasını görmək asandır. q üçün yazılı ifadə qırıq xəttin xarakteristikasını düz xəttlə (şək. 18.1, e) elə bir yamacla əvəz etmək deməkdir ki, bu xətt təqribən a amplitudası ilə əhatə olunan qırıq xəttin kəsiyini əvəz etsin. Buradan (18.18) düsturu ilə veriləndən tərs mütənasib asılılıq tamamilə başa düşüləndir, çünki giriş dəyərinin dalğalanmalarının a amplitudası nə qədər böyükdürsə, qırıq xətti təxminən əvəz edən düz xətt bir o qədər düz olmalıdır.

Vəziyyət Şəkil 1-dəki rele xarakteristikasına bənzəyir. 18.1, r üçün onu əvəz edən xəttin yamacı (18.16) düsturla verilir. Nəticə etibarilə, salınım prosesində hər hansı histerezsiz rele əlaqəsi belə bir “xətti” əlaqəyə bərabərdir, dişli nisbəti (qazanma) giriş dəyişən rəqslərinin amplitudasının artması ilə azalır.

Bir histerezis döngəsi olan rele bağlantısına gəldikdə, (18.9) və (18.17) uyğun olaraq, o, oxşar əvvəlki qazancı olan xətti əlaqə ilə əvəz olunur, lakin əlavə olaraq, sağ tərəfdə mənfi törəmənin tətbiqi ilə. tənlik. Müsbətdən fərqli olaraq mənfi törəmənin tətbiqi (bax § 10.2) giriş hərəkətinə keçidin cavabında bir faza gecikməsini təqdim edir. Bu, qeyri-xəttiliyin histerezis dövrə effektini əvəz edən "xətti ekvivalent" kimi xidmət edir. Harada

(18.17)-ə uyğun törəmədə əmsalı da giriş dəyərinin salınımlarının a amplitudasının artması ilə azalır, bu başa düşüləndir, çünki histerezis dövrəsinin rele keçidindəki salınımlar prosesinə təsiri aşağıdakı kimi olmalıdır. daha kiçik, histerezis döngəsinin eni ilə müqayisədə salınım amplitudası bir o qədər böyükdür.

Digər sadə qeyri-xətti həlqələrin harmonik xəttiləşdirmə əmsalları. Ölü zona və doyma ilə qeyri-xətti əlaqəni nəzərdən keçirək (Şəkil 18.2, a). Şəkilə görə. 18.2, b, harada

kəsiyi üzrə inteqral (18.10) beş həddə bölünür və onlardan ikisi sıfıra bərabərdir. Buna görə də

əvəz ilə haradan alırıq

burada (18.19) düsturları ilə müəyyən edilir. Çünki burada histerezis dövrəsi yoxdur

Beləliklə, formanın xarakteristikası ilə qeyri-xətti əlaqənin tənliyi şək. 18.2 və (18.20) ifadəsi ilə müəyyən edilən yerdə olacaq.

Xüsusi bir hal olaraq, bu, doyma olmadan ölü zona ilə əlaqə üçün bir dəyər verir (Şəkil 18.2, c). Bunu etmək üçün, əvvəlki həlldə biz qoymalıyıq və buna görə də, Sonra

Gördüyünüz kimi, ölü zonası olan bir əlaqə burada onun hesabına qazancı azalan xətti əlaqəyə bənzədilir. Qazancın bu azalması kiçik amplitüdlərdə əhəmiyyətli, böyüklərdə isə kiçikdir

Harmonik xəttiləşdirmə metodu ideyası N.M. Krılov və N.N. Bogolyubov və sistemin qeyri-xətti elementinin xətti əlaqə ilə əvəz edilməsinə əsaslanır, onun parametrləri qeyri-xətti çıxışda birinci harmoniklərin amplitüdlərinin bərabərliyi şərtindən harmonik giriş hərəkəti altında müəyyən edilir. element və onun ekvivalent xətti əlaqə. Bu üsul sistemin xətti hissəsi aşağı keçid filtri olduqda istifadə edilə bilər, yəni. birinci harmonik istisna olmaqla, qeyri-xətti elementin çıxışında yaranan bütün harmonik komponentləri süzür.

Harmonik xəttiləşdirmə əmsalları və qeyri-xətti elementlərin ekvivalent kompleks qazancları. Qeyri-xətti sistemdə (şək. 2.1) xətti hissənin və qeyri-xətti elementin parametrləri elə seçilir ki, tezliyi w olan simmetrik dövri rəqslər mövcud olsun.

Tənlik ilə təsvir edilən qeyri-xəttilərin harmonik xəttiləşdirmə metodunun mərkəzində (Şəkil 2.10)

y n = F(x), (2.17)

qeyri-xətti elementin girişinə w tezliyi və amplituda malik harmonik hərəkətin tətbiq edildiyi fərziyyəsi var. a, yəni.

x= a sin y, burada y = wt, (2.18)

və yalnız birinci harmonik çıxış siqnalının bütün spektrindən fərqlənir

y n 1 = a n 1 günah(y + y n 1), (2.19)

harada a n 1 - amplituda və y n 1 - faza sürüşməsi;

bu halda daha yüksək harmoniklər atılır və çıxış siqnalının birinci harmonikası ilə qeyri-xətti elementin giriş harmonik effekti arasında əlaqə qurulur.

düyü. 2.10. Qeyri-xətti elementin xüsusiyyətləri

Həssaslıq halında qeyri-xətti sistem daha yüksək harmoniklərə qeyri-xətti element birinci yaxınlaşmada ekvivalent qazanclı bəzi elementlə əvəz edilə bilər ki, bu da girişdəki sinusoidal rəqslərin tezliyindən və amplitudasından asılı olaraq çıxışda dövri rəqslərin birinci harmonikasını təyin edir.

(2.17) xarakteristikasına malik qeyri-xətti elementlər üçün dövri funksiya F(x)-in girişdə (2.18) sinusoidal rəqsləri olan Furye sırasına genişləndirilməsi nəticəsində çıxış siqnalının birinci harmonikası üçün ifadə alırıq.

y n 1 = b 1F siny + a 1F rahat, (2.20)

burada b 1F , a 1F - düsturlarla təyin olunan müvafiq olaraq birinci harmonikanın fazadaxili və kvadratura komponentlərinin amplitüdlərini təyin edən Furye seriyasında genişlənmə əmsalları:

px= a w cos y, burada p = d/dt,

onda qeyri-xətti elementin çıxışındakı dövri rəqslərin birinci harmonikası ilə onun girişindəki sinusoidal rəqslər arasındakı əlaqə belə yazıla bilər.

y н 1 = x, (2.21)

burada q = b 1F / a, q¢ = a 1F / a.

Son tənlik deyilir harmonik xəttiləşdirmə tənliyi, və q və q¢ əmsalları - harmonik xəttiləşmə əmsalları.

Beləliklə, qeyri-xətti element harmonik siqnala məruz qaldıqda, daha yüksək harmoniklərə qədər xətti olan (2.21) tənliyi ilə təsvir edilir. Qeyri-xətti elementin bu tənliyi xətti əlaqənin tənliyindən onunla fərqlənir ki, onun q və q¢ əmsalları amplituda dəyişikliyi ilə dəyişir. a və girişdəki rəqslərin tezliyi w. Bu, əmsalları giriş siqnalından asılı olmayan, ancaq qeyri-xətti elementin xarakteristikası növü ilə müəyyən edilən harmonik xəttiləşdirmə ilə adi linearlaşma arasındakı əsas fərqdir.

Qeyri-xətti xüsusiyyətlərin müxtəlif növləri üçün harmonik xəttiləşdirmə əmsalları cədvəldə ümumiləşdirilmişdir. Ümumi halda harmonik xəttiləşmə əmsalları q( a, w) və q¢( a, w) amplitudadan asılıdır a və qeyri-xətti elementin girişindəki rəqslərin tezliyi w. Lakin statik qeyri-xəttilər üçün bu əmsallar q( a) və q¢( a) yalnız amplitudanın funksiyasıdır a giriş harmonik siqnalı və statik birqiymətli qeyri-xəttilər üçün əmsalı q¢( a) = 0.

(2.21) tənliyini sıfır ilkin şərtlər altında Laplas çevrilməsinə tabe edərək və sonra s operatorunu jw (s = jw) ilə əvəz edərək, alırıq ekvivalent kompleks qazanc qeyri-xətti element

W E (jw, a) = q + jq¢ = A e (w, a) e j y e (w , a) , (2.22)

burada ekvivalent kompleks qazancın modulu və arqumenti ifadələrlə harmonik xəttiləşdirmə əmsalları ilə əlaqələndirilir.

A E (w, a) = mod W E (jw, a) =

y E (w, a) = arg W E (jw, A) = arctg.

Qeyri-xətti elementin ekvivalent kompleks ötürmə əmsalı onun girişində harmonik təsir (2.18) altında qeyri-xətti elementin çıxışında birinci harmonikanın (2.19) amplitudasını və faza yerdəyişməsini təyin etməyə imkan verir, yəni.

a n 1 = a´A E (w, a); y n 1 \u003d y E (w, a).

Qeyri-xətti sistemlərdə simmetrik dövri rejimlərin tədqiqi. Harmonik xəttiləşdirmə üsuluna əsaslanan qeyri-xətti sistemlərin tədqiqində ilk növbədə dövri rejimlərin mövcudluğu və sabitliyi məsələsi həll edilir. Əgər dövri rejim sabitdirsə, o zaman sistemdə w 0 tezliyi və amplitudalı öz-özünə salınımlar olur. a 0 .

Transfer funksiyası olan xətti hissəni ehtiva edən qeyri-xətti sistemi (şək. 2.5) nəzərdən keçirək

və ekvivalent kompleks qazancı olan qeyri-xətti element

W E (jw, a) = q(w, a) + jq¢(w, a) = A E (w, a) e j y e (w , a) . (2.24)

(2.21) ifadəsini nəzərə alaraq qeyri-xətti sistemin tənliyini yaza bilərik

(A(p) + B(p)´)x = 0. (2.25)

Əgər qapalı qeyri-xətti sistemdə öz-özünə rəqslər baş verərsə

x= a 0 günah w 0 t

sabit amplituda və tezlik ilə, sonra harmonik xəttiləşdirmə əmsalları sabit olur və bütün sistem stasionar olur. Harmonik xəttiləşdirmə metodundan istifadə edərək qeyri-xətti sistemdə öz-özünə salınmaların mümkünlüyünü qiymətləndirmək üçün xətti sistemlərin dayanıqlığının təhlilində edildiyi kimi, sabitlik sərhədi üçün şərtləri tapmaq lazımdır. Əgər dövri həll mövcuddur a = a 0 və w = w 0 harmonik xəttiləşdirilmiş sistemin xarakterik tənliyi

A(p) + B(p)´ = 0 (2.26)

l i = jw 0 və l i +1 = -jw 0 cüt xəyali köklərə malikdir. Həllin sabitliyini əlavə olaraq qiymətləndirmək lazımdır.

Xarakterik tənliyin həlli üsullarından asılı olaraq qeyri-xətti sistemlərin öyrənilməsi üsulları fərqləndirilir.

Analitik metod . Qeyri-xətti sistemdə öz-özünə salınmaların mümkünlüyünü qiymətləndirmək üçün p əvəzinə sistemin harmonik xəttiləşdirilmiş xarakterik polinomuna jw əvəz edilir.

D(jw, a) = A(jw) + B(jw)´. (2,27)

Nəticə D(jw,) tənliyidir. a) = 0, onun əmsalları fərz edilən öz-özünə salınan rejimin amplitudasından və tezliyindən asılıdır. Həqiqi və xəyali hissələrin ayrılması

Re D(jw, a) = X(w, a);

Im D(jw, a) = Y(w, a),

tənliyini alırıq

X(w, a) + jY(w, a) = 0. (2.28)

Əgər real dəyərlər üçün a 0 və w 0 ifadəsi (2.28) yerinə yetirildikdə, sistemdə parametrləri aşağıdakı tənliklər sisteminə görə hesablanan öz-özünə salınan rejim mümkündür:

(2.29) ifadələrindən, sistemin parametrlərindən, məsələn, sistemin xətti hissəsinin k ötürmə əmsalından öz-özünə salınmaların amplitüdünün və tezliyinin asılılığını tapmaq olar. Bunun üçün (2.29) tənliklərində k transfer əmsalını dəyişən kimi nəzərə almaq lazımdır, yəni. bu tənlikləri formada yazın:

Qrafiklərə görə a 0 = f (k), w 0 = f (k), siz k transfer əmsalını seçə bilərsiniz, bu zaman mümkün öz-özünə salınmaların amplitudası və tezliyi məqbul dəyərlərə malikdir və ya tamamilə yoxdur.

tezlik metodu. Nyquist sabitlik meyarına uyğun olaraq, xətti sistemdə sönümsüz rəqslər açıq dövrəli sistemin amplituda-faza xarakteristikasının koordinatları [-1, j0] olan nöqtədən keçdiyi zaman yaranır. Bu şərt həm də harmonik şəkildə xəttiləşmiş qeyri-xətti sistemdə öz-özünə rəqslərin mövcudluğu üçün şərtdir, yəni.

W n (jw, a) = -1. (2.31)

Sistemin xətti və qeyri-xətti hissələri ardıcıl olaraq bağlandığından, açıq dövrəli qeyri-xətti sistemin tezlik reaksiyası belədir.

W n (jw, a) = W lch (jw)'W E (jw, a). (2.32)

Sonra qeyri-xətti elementin statik xarakteristikası olduqda (2.31) şərti formanı alır.

W lch (jw) = - . (2.33)

(2.33) tənliyinin öz-özünə salınmaların tezliyinə və amplitudasına görə həllini sistemin W lch (jw) xətti hissəsinin tezlik reaksiyasının hodoqrafının kəsişmə nöqtəsi kimi qrafik şəkildə əldə etmək olar. əks işarə ilə götürülmüş qeyri-xətti hissənin tərs xarakteristikası (şək. 2.11). Əgər bu hodoqraflar kəsişmirsə, o zaman tədqiq olunan sistemdə öz-özünə salınma rejimi mövcud deyildir.

düyü. 2.11. Sistemin xətti və qeyri-xətti hissələrinin hodoqrafları

Tezliyi w 0 və amplituda olan öz-özünə salınan rejimin sabitliyi üçün a 0 tələb olunur ki, qeyri-xətti hissənin hodoqrafındakı nöqtə - , artan amplituda uyğundur a 0+D a hodoqrafların kəsişmə nöqtəsindəki qiymətlə müqayisədə sistemin xətti hissəsinin tezlik reaksiyasının hodoqrafı ilə əhatə olunmamışdır və azaldılmış amplituda uyğun olan nöqtə əhatə edilmişdir. a 0-D a.

Əncirdə. 2.11 qeyri-xətti sistemdə sabit öz-özünə rəqslərin mövcud olduğu hal üçün hodoqrafların yerləşməsinə dair bir nümunə verir, çünki a 3 < a 0 < a 4 .

Loqarifmik tezlik reaksiyalarının öyrənilməsi.

Qeyri-xətti sistemləri loqarifmik tezlik xarakteristikaları ilə öyrənərkən açıq dövrəli qeyri-xətti sistemin ekvivalent kompleks qazancının modulu və arqumenti üçün şərt (2.31) ayrıca yenidən yazılır.

mod W lch (jw)W e (jw, a) = 1;

arg W lch (jw)W e (jw, a) = - (2k+1)p, k=0, 1, 2, ... üçün

sonradan loqarifmik amplituda və faza xüsusiyyətlərinə keçid ilə

L h (w) + L e (w, a) = 0; (2.34)

y lch (w) + y e (w, a) = - (2k+1)p, k=0, 1, 2, ... üçün (2.35)

(2.34) və (2.35) şərtləri amplitudu təyin etməyə imkan verir a L lch (w), y lch (w) sisteminin xətti hissəsinin və L e (w,) qeyri-xətti elementinin loqarifmik xüsusiyyətlərinə görə (2.25) tənliyinin dövri həllinin 0 və tezliyi w 0. a), y e (w, a).

Tezliyi w 0 və amplituda olan öz-özünə salınımlar a(2.25) tənliyinin dövri həlli sabit olarsa, 0 qeyri-xətti sistemdə mövcud olacaqdır. Dövri həllin sabitliyini öyrənmək üçün təxmini üsul, sistemin w = w 0 tezliyində və amplituda qiymətlərində davranışını öyrənməkdir. a =a 0+D a Və a =a 0-D a, harada D a> 0 - kiçik amplituda artımı. Üçün dövri həllin dayanıqlığını öyrənərkən a 0+D a Və a 0-D a loqarifmik xüsusiyyətlərə görə, Nyquist sabitlik meyarından istifadə olunur.

Qeyri-xətti elementin birqiymətli statik xarakteristikası olan qeyri-xətti sistemlərdə harmonik xəttiləşmə əmsalı q¢( a) sıfıra bərabərdir və buna görə də sıfıra bərabərdir və faza sürüşməsi y e ( a) elementi ilə töhfə verir. Bu halda sistemin tənliyinin dövri həlli

x = 0 (2,36)

aşağıdakı şərtlər yerinə yetirildikdə mövcuddur:

L h (w) \u003d - L e ( a); (2.37)

y lch (w) = - (2k+1)p, k=0, 1, 2, ... (2.38) üçün

Tənlik (2.38) bizə dövri həllin tezliyini w \u003d w 0, tənlik (2.37) isə onun amplitudunu təyin etməyə imkan verir. a =a 0 .

Nisbətən sadə xətti hissə ilə bu tənliklərin həlli analitik yolla əldə edilə bilər. Lakin əksər hallarda onları qrafik şəkildə həll etmək məqsədəuyğundur (şək. 2.12).

(2.36) tənliyinin dövri həllinin dayanıqlığını öyrənərkən, yəni. tək qiymətli qeyri-xətti statik xarakteristikaya malik qeyri-xətti sistemdə öz-özünə salınımların mövcudluğunu təyin edərkən, istifadə olunur. Nyquist meyarı: tezliyi w = w 0 və amplituda olan dövri həll a =a Tezlik sıfırdan sonsuza qədər dəyişdikdə və D amplitudasının müsbət artımı olduqda 0 sabitdir. a> 0 -p xətti ilə sistemin y lch (w) xətti hissəsinin faza xarakteristikasının müsbət (yuxarıdan aşağı) və mənfi (aşağıdan yuxarı) keçidlərinin sayı arasındakı fərq tezlikdə sıfırdır. diapazon, burada L lch (w)³-L e (w 0 , a 0+D a), və tezlik diapazonunda sıfıra bərabər deyil, burada L h (w)³-L e (w 0, a 0-D a).

Əncirdə. 2.12 məhdudiyyətli qeyri-xətti sistemdə dövri həllərin təyin edilməsi nümunəsini göstərir. Belə bir sistemdə, faza xarakteristikasının y lch (w) -180 0 xətti ilə kəsişmə nöqtələrində təyin olunan w 01 , w 02 və w 03 tezlikləri olan üç dövri həll var. Periodik həll amplitüdləri a 01 , a 02 və a 03 qeyri-xətti elementin -L e (w 01 ,) loqarifmik amplituda xarakteristikaları ilə (2.37) şərtindən müəyyən edilir. a), -L e (w 02, a) və -L e (w 03, a).

düyü. 2.12. Loqarifmik amplituda və faza xüsusiyyətləri

Şəkildə göstərilən üç həlldən. 2.12, ikisi sabitdir. Tezliyi w = w 01 və amplituda olan həll a =a 01 sabitdir, çünki 1 tezlik diapazonunda, burada L lch (w)³-L e (w 01, a 01+D a), faza xarakteristikası y lch (w) -180 0 xəttini keçmir, lakin 2 tezlik diapazonunda, burada L lch (w)³-L e (w 01, a 01-D a), faza xarakteristikası y lch (w) bir dəfə -180 0 xəttini keçir. Tezliyi w = w 02 və amplituda olan həll a =a 02 qeyri-sabitdir, çünki L h (w)³-L e (w 02, a 02+D a), faza xarakteristikası y lch (w) bir dəfə -180 0 xəttini keçir. Tezliyi w = w 03 və amplituda olan yüksək tezlikli dövri həll a =a 03 sabitdir, çünki tezlik diapazonunda L h (w)³-L e (w 03, a 03+D a), -180 0 xətti ilə y lch (w) faza xarakteristikasının bir müsbət və bir mənfi keçidi və L lch (w)³-L e (w 03, a 03-D a), -180 0 xətti ilə faza xarakteristikasının y lch (w) iki müsbət və bir mənfi keçidi var.

Nəzərdə tutulan sistemdə kiçik təlaşlarla, w 03 tezliyi və amplitudalı yüksək tezlikli öz-özünə salınımlar a 03 , və böyük təlaşlar üçün - w 01 tezliyi və amplituda ilə aşağı tezlikli öz-özünə salınımlar a 01 .

Misal. Xətti hissəsi aşağıdakı ötürmə funksiyasına malik olan qeyri-xətti sistemdə öz-özünə salınan rejimləri araşdırın.

burada k=200 s -1 ; T 1 =1,5 s; T 2 \u003d 0,015 s,

qeyri-xətti element kimi isə c=10 V, b=2 V-də ölü zonalı rele istifadə olunur (şək. 2.4, b).

Həlli.Ölü zonalı rele üçün cədvələ əsasən harmonik xəttiləşdirmə əmsallarını tapırıq:

At a³ b, q¢( a) = 0.

Qeyri-xətti elementin xarakteristikalarını qurarkən giriş harmonik effektinin amplitudasının nisbi qiymətini istifadə etmək məqsədəuyğundur m = a/b. Harmonik xəttiləşmə əmsalı üçün ifadəni formada yenidən yazaq

relenin ötürmə əmsalı haradadır;

Nisbi amplituda.

Rele ötürmə əmsalı k n sistemin xətti hissəsi ilə əlaqədardır və biz normallaşdırılmış harmonik xəttiləşdirmə əmsallarını alırıq.

və əks işarəli rele elementinin normallaşdırılmış loqarifmik amplituda xarakteristikası

Əgər m ® 1, onda -L e (m) ® ¥; və m >> 1 -L e (m) = 20 lg m olduqda. Beləliklə, əks işarəli normallaşdırılmış loqarifmik amplituda xarakteristikasının asimptotları koordinatları L = 0, m = 1 olan nöqtədən keçən şaquli düz xətt və mailliyi +20 dB/dek olan düz xəttdir (Şəkil 2). 2.13).

düyü. 2.13. Rele sistemində dövri həllin təyini

ölü zona ilə

a 0 = b´m 1 = = 58 V.

Qeyri-xətti elementin əks işarəsi və sistemin xətti hissəsinin ötürmə funksiyası ilə normallaşdırılmış loqarifmik amplituda xarakteristikasına uyğun olaraq öz-özünə salınmaların mövcudluğu məsələsini həll etmək.

şək. 2.13 L ch (w), -L e (m) və y ch (w) loqarifmik xarakteristikalarının qrafikini çəkdi.

Dövri məhlulun tezliyi w 0 = 4.3 s -1 faza xarakteristikasının y lch (w) ilə -180 0 xəttinin kəsişmə nöqtəsində müəyyən edilir. Dövri məhlulların m 1 = 29 və m 2 = 1,08 amplitüdləri L h (w) və -L e (m) xüsusiyyətlərinə görə tapılır. Kiçik amplituda m 2 olan dövri məhlul qeyri-sabitdir, böyük amplituda m 1 olan dövri həll isə sabitdir.

Beləliklə, tədqiq olunan rele sistemində w 0 = 4,3 s -1 tezliyi və amplitudalı öz-özünə salınan rejim mövcuddur. a 0 = b´m 1 = = 58 V.

Rusiya Federasiyasının Təhsil və Elm Nazirliyi

Saratov Dövlət Texniki Universiteti

Balakovo Mühəndislik, Texnologiya və İdarəetmə İnstitutu

Harmonik xəttiləşdirmə üsulu

“Nəzəriyyə” kursu üzrə laboratoriya işi üçün göstərişlər avtomatik nəzarət» 210100 ixtisasının tələbələri üçün

Təsdiq edildi

redaksiya və nəşriyyat şurası

Balakovo Texnologiya İnstitutu,

texnologiya və idarəetmə

Balakovo 2004

İşin məqsədi: Harmonik xəttiləşdirmə (harmonik tarazlıq) üsulu ilə qeyri-xətti sistemlərin tədqiqi, müxtəlif qeyri-xətti həlqələr üçün harmonik xəttiləşmə əmsallarının təyini. Sabit amplituda və tezliyin simmetrik rəqslərinin (öz-özünə salınımların) parametrlərini tapmaq, cəbri, tezlik üsullarından istifadə etməklə, həmçinin Mixaylov meyarından istifadə etmək bacarıqlarının əldə edilməsi.

ƏSAS MƏLUMAT

Harmonik xəttiləşdirmə metodu qeyri-xətti sistemləri öyrənmək üçün təxmini üsullara aiddir. Bu, qeyri-xətti sistemlərin dayanıqlığını kifayət qədər sadə və məqbul dəqiqliklə qiymətləndirməyə, sistemdə qurulmuş rəqslərin tezliyini və amplitudasını təyin etməyə imkan verir.

Tədqiq olunan qeyri-xətti ACS-nin aşağıdakı formada təqdim oluna biləcəyi güman edilir

üstəlik, qeyri-xətti hissənin bir qeyri-xəttiliyi olmalıdır

. (1)

Bu qeyri-xəttilik ya davamlı, ya da relay, birmənalı və ya histeretik ola bilər.

İstənilən funksiya və ya siqnal xətti müstəqil, konkret halda ortonormal funksiyalar sisteminə uyğun olaraq seriyaya genişləndirilə bilər. Belə bir ortoqonal sıra kimi Furye seriyasından istifadə etmək olar.

Sistemin qeyri-xətti hissəsinin çıxış siqnalını Furye seriyasına genişləndirək

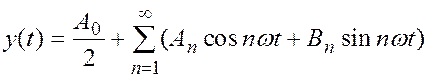, (2)

burada Furye əmsalları,

. (3)

Beləliklə, (2) bəndinə uyğun olaraq siqnal artan tezliklərlə harmoniklərin sonsuz cəmi kimi təqdim edilə bilər. Bu siqnal qeyri-xətti sistemin xətti hissəsinə daxil edilir.

Xətti hissənin ötürmə funksiyasını işarə edək

, (4)

və paylayıcı çoxhədlinin dərəcəsi məxrəc çoxhədlinin dərəcəsindən kiçik olmalıdır. Bu halda xətti hissənin tezlik reaksiyası formaya malikdir

burada 1 - dirək yoxdur, 2 - dirək və ya dirək var.

Tezlik cavabı üçün yazmaq ədalətlidir

Beləliklə, qeyri-xətti sistemin xətti hissəsi yüksək keçid filtridir. Bu halda xətti hissə zəifləmədən yalnız aşağı tezlikləri keçəcək, yüksək tezliklər isə tezlik artdıqca əhəmiyyətli dərəcədə zəifləyəcək.

Harmonik xəttiləşdirmə üsulu, sistemin xətti hissəsinin yalnız siqnalın DC komponentindən və birinci harmonikdən keçəcəyini nəzərdə tutur. Sonra xətti hissənin çıxışındakı siqnal belə görünəcəkdir

Bu siqnal sistemin bütün qapalı dövrəsindən keçir Fig.1 və qeyri-xətti elementin çıxışında daha yüksək harmonikləri nəzərə almadan (2)-ə uyğun olaraq

. (7)

Harmonik xəttiləşdirmə metodundan istifadə edərək qeyri-xətti sistemlərin tədqiqində simmetrik və asimmetrik rəqslər halları mümkündür. Simmetrik rəqslər halını nəzərdən keçirək. Burada və.

Aşağıdakı qeydi təqdim edirik

Onları (7) ilə əvəz edərək, əldə edirik. (8)

Bunu nəzərə alaraq

, harada,

. (9)

(3) və (8) bəndlərinə əsasən

. (10)

İfadə (9) qeyri-xəttiliyin harmonik xəttiləşdirilməsidir -də giriş dəyişəni ilə çıxış dəyişəni arasında xətti əlaqə qurur. və kəmiyyətlərinə harmonik linearlaşma əmsalları deyilir.

Qeyd etmək lazımdır ki, tənlik (9) xüsusi dəyərlər və (sistemdəki harmonik salınımların amplitüdləri və tezlikləri) üçün xəttidir. Amma ümumilikdə qeyri-xətti xassələri saxlayır, çünki əmsallar müxtəlif və üçün fərqlidir. Bu xüsusiyyət harmonik xəttiləşdirmə metodundan istifadə edərək qeyri-xətti sistemlərin xassələrini tədqiq etməyə imkan verir [Popov E.P.].

Asimmetrik rəqslər vəziyyətində qeyri-xəttiliyin harmonik linearlaşması xətti tənliyə gətirib çıxarır.

. (12)

Eynilə (9) tənliyi kimi, xəttiləşdirilmiş tənlik (11) qeyri-xətti elementin xassələrini saxlayır, çünki harmonik xəttiləşmə əmsalları , eləcə də sabit komponent harmonik rəqslərin həm yerdəyişməsindən, həm də amplitudasından asılıdır.

(9) və (11) tənlikləri harmonik xəttiləşdirilmiş qeyri-xətti elementlərin ötürmə funksiyalarını əldə etməyə imkan verir. Beləliklə, simmetrik vibrasiya üçün

Rusiya Federasiyasının Təhsil və Elm Nazirliyi

Saratov Dövlət Texniki Universiteti

Balakovo Mühəndislik, Texnologiya və İdarəetmə İnstitutu

Harmonik xəttiləşdirmə üsulu

üçün təlimatlar laboratoriya işi 210100 ixtisasının tələbələri üçün “Avtomatik idarəetmə nəzəriyyəsi” kursu üzrə

Təsdiq edildi

redaksiya və nəşriyyat şurası

Balakovo Texnologiya İnstitutu,

texnologiya və idarəetmə

Balakovo 2004

ƏSAS MƏLUMAT

Tədqiq olunan qeyri-xətti ACS-nin aşağıdakı formada təqdim oluna biləcəyi güman edilir

üstəlik, qeyri-xətti hissənin bir qeyri-xəttiliyi olmalıdır

Bu qeyri-xəttilik ya davamlı, ya da relay, birmənalı və ya histeretik ola bilər.

Sistemin qeyri-xətti hissəsinin çıxış siqnalını Furye seriyasına genişləndirək

, (2)

burada Furye əmsalları,

. (3)

Beləliklə, (2) bəndinə uyğun olaraq siqnal artan tezliklərlə harmoniklərin sonsuz cəmi kimi təqdim edilə bilər. Bu siqnal qeyri-xətti sistemin xətti hissəsinə daxil edilir.

Xətti hissənin ötürmə funksiyasını işarə edək

, (4)

və paylayıcı çoxhədlinin dərəcəsi məxrəc çoxhədlinin dərəcəsindən kiçik olmalıdır. Bu halda xətti hissənin tezlik reaksiyası formaya malikdir

burada 1 - dirək yoxdur, 2 - dirək və ya dirək var.

Tezlik cavabı üçün yazmaq ədalətlidir

Bu siqnal sistemin bütün qapalı dövrəsindən keçir Fig.1 və qeyri-xətti elementin çıxışında daha yüksək harmonikləri nəzərə almadan (2)-ə uyğun olaraq

. (7)

Aşağıdakı qeydi təqdim edirik

Onları (7) ilə əvəz edərək, əldə edirik. (8)

Bunu nəzərə alaraq

. (9)

(3) və (8) bəndlərinə əsasən

. (10)

İfadə (9) qeyri-xəttiliyin harmonik xəttiləşdirilməsidir və giriş dəyişəni ilə çıxış dəyişəni arasında xətti əlaqə qurur. və kəmiyyətlərinə harmonik linearlaşma əmsalları deyilir.

Asimmetrik rəqslər vəziyyətində qeyri-xəttiliyin harmonik linearlaşması xətti tənliyə gətirib çıxarır.

. (12)

(9) və (11) tənlikləri harmonik xəttiləşdirilmiş qeyri-xətti elementlərin ötürmə funksiyalarını əldə etməyə imkan verir. Beləliklə, simmetrik vibrasiya üçün

, (13)

tezlik ötürmə funksiyası isə

yalnız amplitudadan asılıdır və sistemdəki rəqslərin tezliyindən asılı deyil.

Qeyd etmək lazımdır ki, əgər tək-simmetrik qeyri-xətti birqiymətlidirsə, onda simmetrik rəqslər zamanı (9) və (10) bəndlərinə uyğun olaraq, alırıq ki, , (15)

(16)

xəttiləşmiş qeyri-xəttilik isə formaya malikdir

Qeyri-müəyyən qeyri-xəttilər üçün (histerezisi ilə) ifadədə (16) inteqral sıfra bərabər deyil, artan və azalan əyrinin davranışındakı fərqə görə , buna görə də tam ifadə (9) etibarlıdır.

Bəzi qeyri-xətti xarakteristikalar üçün harmonik xəttiləşdirmə əmsallarını tapaq. Qeyri-xətti xarakteristika histerezisi və ölü zonası olan rele xarakteristikasının formasını alsın. Belə bir xüsusiyyətə malik qeyri-xətti elementdən harmonik rəqslərin necə keçdiyini düşünün.



Şərt yerinə yetirildikdə, yəni giriş siqnalının amplitudası ölü zonadan azdırsa, o zaman qeyri-xətti elementin çıxışında siqnal yoxdur. Əgər amplituda olarsa, rele A, B, C və D nöqtələrində keçir. Və işarələyin.

. (18)

Harmonik xəttiləşdirmə əmsallarını hesablayarkən nəzərə almaq lazımdır ki, simmetrik qeyri-xətti xüsusiyyətləri ilə (10) ifadələrindəki inteqrallar nəticənin iki dəfə artması ilə yarım dövrədə (0, ) olur. . Bu cür

. (19)

Röle xarakteristikası və ölü zonası olan qeyri-xətti element üçün

Histerezisi olan rele xarakteristikasına malik qeyri-xətti element üçün

Digər qeyri-xətti xarakteristikalar üçün harmonik xəttiləşdirmə əmsalları eyni şəkildə əldə edilə bilər.

Sabit amplituda və tezliyin simmetrik rəqslərini (öz-özünə rəqslər) və xəttiləşdirilmiş sistemlərin sabitliyini təyin etmək üçün iki metodu nəzərdən keçirək: cəbri və tezliyi. Əvvəlcə cəbri yola baxaq. Qapalı sistem üçün Fig.1, xətti hissənin ötürmə funksiyası bərabərdir

Qeyri-xətti hissənin harmonik xəttiləşdirilmiş ötürmə funksiyasını yazırıq

Qapalı sistemin xarakterik tənliyi formaya malikdir

. (22)

Tədqiq olunan sistemdə öz-özünə salınımlar baş verirsə, bu, onun xarakterik tənliyində iki sırf xəyali kökün olduğunu göstərir. Buna görə də, xarakterik tənliyə (22) kökün qiymətini əvəz edirik.

. (23)

Təsəvvür edin

İstədiyiniz amplituda və tezliyi təyin edən iki tənlik alırıq

. (24)

Həlldə amplituda və tezliyin həqiqi müsbət dəyərləri mümkündürsə, sistemdə öz-özünə salınımlar baş verə bilər. Əgər amplituda və tezlik müsbət dəyərlərə malik deyilsə, o zaman sistemdə öz-özünə salınımlar qeyri-mümkündür.

Nümunə 1-i nəzərdən keçirək. Tədqiq olunan qeyri-xətti sistemin forması olsun

Bu misalda qeyri-xətti element harmonik xəttiləşdirmə əmsallarının rele xarakteristikasına malik hissedici elementdir.

Aktuator formanın ötürmə funksiyasına malikdir

Tənzimlənən obyektin ötürmə funksiyası bərabərdir

. (27)

Sistemin xətti hissəsinin ötürmə funksiyası

, (28)

(22), (25) və (28) əsasında qapalı sistemin xarakterik tənliyini yazırıq.

, (29)

1/san, san, san, c.

Bu halda dövri hərəkətin parametrləri bərabərdir

7,071 ,

Mixaylov meyarından istifadə edərək xəttiləşdirilmiş ACS-də öz-özünə salınmaların parametrlərinin təyin edilməsi üsulunu nəzərdən keçirək. Metod ona əsaslanır ki, öz-özünə salınımlar baş verdikdə, sistem sabitlik sərhəddində olacaq və bu halda Mixaylov hodoqrafı mənbədən keçəcəkdir.

2-ci misalda biz öz-özünə rəqslərin parametrlərini bir şərtlə tapırıq ki, sistemdəki qeyri-xətti element Şəkil 4 histerezisi olan rele xarakteristikasına malik olan həssas elementdir, onun üçün harmonik xəttiləşmə əmsalları

Xətti hissə dəyişməz qaldı.

Qapalı sistemin xarakterik tənliyini yazırıq

Mixaylov hodoqrafı əvəz etməklə əldə edilir.

Vəzifə hodoqrafın koordinatların mənşəyindən keçdiyi salınımların belə bir amplitüdünü seçməkdir. Qeyd etmək lazımdır ki, bu halda cari tezlik , çünki bu halda əyri başlanğıcdan keçəcəkdir.

MATHCAD 7 proqramında 1/san, s, s, in və in-də aparılan hesablamalar aşağıdakı nəticələri verdi. Şəkil 5-də Mixaylovun hodoqrafı mənbədən keçir. Hesablamaların düzgünlüyünü artırmaq üçün qrafikin istədiyiniz fraqmentini artıracağıq. Şəkil 6-da mənşənin yaxınlığında böyüdülmüş hodoqraf fraqmenti göstərilir. Əyri koordinatların başlanğıcından keçir.

Şəkil 5. Şəkil 6.

Bu halda, modulun sıfıra bərabər olması şərtindən titrəmə tezliyini tapmaq olar. Tezliklər üçün

modul dəyərləri cədvəl şəklində verilmişdir

Beləliklə, rəqs tezliyi 6,38-dir. Qeyd etmək lazımdır ki, hesablamaların dəqiqliyi asanlıqla artırıla bilər.

Amplituda və tezliyin dəyəri ilə müəyyən edilən dövri həll sabitlik üçün araşdırılmalıdır. Əgər həll stabildirsə, o zaman sistemdə öz-özünə salınan proses (sabit limit dövrü) baş verir. Əks halda, limit dövrü qeyri-sabit olacaq.

Dövri həllin dayanıqlığını öyrənməyin ən asan yolu qrafik formada Mixaylov sabitlik meyarından istifadə etməkdir. Məlum olmuşdur ki, , -də Mixaylov əyrisi koordinatların başlanğıcından keçir. Kiçik bir artım versəniz, əyri ya sıfırdan yuxarı, ya da aşağıda bir mövqe tutacaq. Beləliklə, sonuncu misalda artıraq, yəni və . Mixaylov əyrilərinin mövqeyi Fig.7-də göstərilmişdir.

-də əyri sıfırdan yuxarı keçir, bu sistemin dayanıqlığını və sönümlənmiş keçid prosesini göstərir. Mixaylov əyrisi sıfırdan aşağı keçəndə sistem qeyri-sabitdir və keçid divergentdir. Beləliklə, amplitudası 6 və salınım tezliyi 6,38 olan dövri həll sabitdir.

Dövri məhlulun dayanıqlığını öyrənmək üçün Mixaylov qrafik kriteriyasından alınan analitik meyardan da istifadə etmək olar. Həqiqətən də, Mixaylov əyrisinin sıfırdan yuxarı gedəcəyini öyrənmək üçün koordinatların başlanğıcında yerləşən Mixaylov əyrisinin nöqtəsinin hara hərəkət edəcəyinə baxmaq kifayətdir.

Bu nöqtənin X və Y koordinat oxları boyunca yerdəyişməsini genişləndirsək, dövri həllin sabitliyi üçün koordinat oxlarına proyeksiyalar tərəfindən təyin olunan vektor.

istiqaməti proyeksiyalarla müəyyən edilən artım istiqamətində əyri boyunca baxıldıqda Mixaylov əyrisinə toxunan MN-nin sağında yerləşməlidir.

Analitik sabitlik şərtini aşağıdakı formada yazaq

Bu ifadədə Mixaylov əyrisinin cari parametrinə görə qismən törəmələr götürülür.

Qeyd etmək lazımdır ki, sabitlik meyarının (31) analitik ifadəsi yalnız dördüncü dərəcədən yüksək olmayan sistemlər üçün etibarlıdır, çünki, məsələn, başlanğıcda beşinci dərəcəli sistem üçün şərt (31) təmin edilə bilər, və sistem qeyri-sabit olacaq

Nümunə 1-də alınan dövri məhlulun dayanıqlığını öyrənmək üçün (31) meyarını tətbiq edirik.

, ,

Giriş

Avtomatik idarəetmə praktikasında rele sistemlərindən geniş istifadə olunur. Rele sistemlərinin üstünlüyü dizaynın sadəliyi, etibarlılığı, texniki xidmətin asanlığı və konfiqurasiyadır. Relay sistemləri qeyri-xətti ACP-lərin xüsusi sinfidir.

Röle sistemlərindəki davamlıdan fərqli olaraq, relenin idarəetmə siqnalı (əksər hallarda bu idarəetmə xətasıdır) bəzi sabit (ərəfəsində) dəyərlərdən, məsələn, sıfırdan keçdikdə idarəetmə hərəkəti kəskin şəkildə dəyişir.

Röle sistemləri, bir qayda olaraq, onlarda idarəetmə hərəkətinin demək olar ki, dərhal dəyişməsi və aktuatorda maksimum amplituda hissə-hissə sabit siqnalın hərəkət etməsi səbəbindən yüksək sürətə malikdir. Eyni zamanda, rele sistemlərində tez-tez öz-özünə salınmalar baş verir ki, bu da bir çox hallarda çatışmazlıqdır. Bu yazıda biz dörd fərqli idarəetmə qanunu olan rele sistemini öyrənirik.

Tədqiq olunan sistemin strukturu

Tədqiq olunan sistemə (Şəkil) 1 ES müqayisə elementi, RE rele elementi, aktuator (qazanma = 1 olan ideal inteqrator), idarəetmə obyekti (üç zaman sabiti ilə aperiodik əlaqə , və qazanc) daxildir. . Sistem parametrlərinin dəyərləri Cədvəldə verilmişdir. 1 əlavə A.

Tədqiq olunan rele elementlərinin statik xarakteristikası (giriş-çıxış xüsusiyyətləri) şək. 2.

Əncirdə. 2,a şəklə ideal iki mövqeli relenin xüsusiyyətlərini göstərir. Ölü zona ilə üç mövqeli relenin 2b xarakteristikası. Əncirdə. 2c və 2d müvafiq olaraq müsbət və mənfi histerezisi olan iki mövqeli relenin xüsusiyyətlərini göstərir.

Tədqiq olunan ACP SIAM və ya VisSim kimi tanınmış modelləşdirmə paketlərindən istifadə etməklə modelləşdirilə bilər.

Şərh. Bəzi simulyasiya paketlərində çıxışın dəyəri

rele siqnalı yalnız ±B əvəzinə ±1 dəyərləri qəbul edə bilər, burada B ixtiyari ədəddir. Belə hallarda inteqratorun qazancını -ə bərabər götürmək lazımdır.

İş sifarişi

İşi başa çatdırmaq üçün hər bir tələbə müəllimdən ilkin məlumatların bir versiyasını alır (2-ci bölməyə baxın).

İş iki mərhələdə aparılır.

Birinci mərhələ hesablama tədqiqatıdır (laboratoriyadan kənarda həyata keçirilə bilər).

İkinci mərhələ eksperimentaldır (laboratoriyada aparılır). Bu mərhələdə paketlərdən birinin köməyi ilə birinci mərhələdə hesablanmış rejimlər üçün tədqiq olunan sistemdə keçici proseslər simulyasiya edilir və nəzəri metodların düzgünlüyü yoxlanılır.

Zəruri nəzəri material 4-cü bölmədə təqdim olunur; 5-ci bölmədə nəzarət sualları var.

3.1. Qəsəbə - tədqiqat hissəsi

1. Sistemin xətti hissəsinin amplituda-tezlik və faza-tezlik, real və xəyali xarakteristikası üçün ifadələr alın.

2. Sistemin xətti hissəsinin amplituda-faza xarakteristikasını hesablayın və qurun. Hesablama üçün TAU paketindəki proqramlardan istifadə edin. Mütləq real və xəyali tezlik reaksiya dəyərlərini çap edin(10 - 15 bal uyğundur üçüncü və ikinci kvadrantlar).

4. Qoldfarbın qrafik-analitik metodundan istifadə edərək, öz-özünə rəqslərin amplitudasını və tezliyini və bütün dörd rele üçün onların sabitliyini təyin edin. Öz-özünə salınma parametrləri də analitik olaraq hesablana bilər. Hər bir hal üçün sistemin faza portretini keyfiyyətcə təsvir edin.

5. Üç mövqeli rele üçün, öz-özünə salınımların olmadığı xətti hissənin qazancının bir qiymətini və öz-özünə salınımların dayandığı sərhəd qiymətini təyin edin.

eksperimental hissə

1. Mövcud simulyasiya paketlərindən birini istifadə edərək, tədqiq olunan ACP-nin simulyasiya sxemini yığın. Müəllimin icazəsi ilə bitmiş sxemdən istifadə edə bilərsiniz. Tapşırıqa uyğun olaraq sxem parametrlərini təyin edin.

2. Girişə x(t)=40*1(t) sıçrayış hərəkəti tətbiq edərək, ideal releli sistemdə keçici prosesi tədqiq edin (çap edin). Öz-özünə salınmaların amplitudasını və tezliyini ölçün, onları hesablanmış dəyərlərlə müqayisə edin. Sıfırdan fərqli ilkin şərtlər qoyaraq təcrübəni təkrarlayın (məsələn, y(0)=10, y(1)(0)=-5).

3. Giriş siqnalının amplitudasının x(t)= 40*1(t) və x(t)=15*1(t) iki fərqli dəyəri üçün üç mövqeli releli sistemdə keçid prosesini araşdırın. Keçici prosesləri çap edin, öz-özünə salınmaların amplitudasını və tezliyini ölçün (əgər onlar varsa), onları hesablanmış dəyərlərlə müqayisə edin və nəticə çıxarın.

4. Xətti hissənin qazancının digər dəyərləri üçün üç mövqeli releli sistemdə keçici prosesləri araşdırın (bax 5-ci bənd, 3.1-ci bölmə).

5. Sıfır və sıfırdan fərqli ilkin şərtlərdə histerezisi olan və x(t)=40*1(t) olan iki mövqeli releli sistemdə keçici prosesləri tədqiq edin. Keçici prosesləri çap edin, öz-özünə salınmaların amplitudasını və tezliyini ölçün (əgər onlar varsa), onları hesablanmış dəyərlərlə müqayisə edin və nəticə çıxarın.

Nəzəri hissə

Qeyri-xətti sistemlərin hesablanması üçün geniş istifadə olunan üsul harmonik xəttiləşdirmə metodudur (funksiyaların təsviri).

Metod, öz-özünə salınmaların parametrlərini (amplituda və tezlik), özünü salınımların sabitliyini və qeyri-xətti ACP-nin tarazlıq vəziyyətinin sabitliyini təyin etməyə imkan verir. Harmonik xəttiləşdirmə metodu əsasında keçici proseslərin qurulması, qeyri-xətti ASR-nin təhlili və sintezi üsulları işlənib hazırlanmışdır.

Harmonik xəttiləşdirmə üsulu

Artıq qeyd edildiyi kimi, qeyri-xətti və xüsusən də releli ACP-lərdə tez-tez müşahidə olunur sabit dövri salınımlar sabit amplituda və tezlik, sözdə öz-özünə salınımlar. Üstəlik, sistem parametrlərində əhəmiyyətli dəyişikliklər olsa belə, öz-özünə salınımlar davam edə bilər. Təcrübə göstərir ki, bir çox hallarda tənzimlənən dəyərin dalğalanmaları (şəkil 3) harmonikə yaxındır.

Öz-özünə salınmaların harmoniklərə yaxınlığı onların parametrlərini – A amplitudasını və w 0 tezliyini təyin etmək üçün harmonik xəttiləşdirmə metodundan istifadə etməyə imkan verir. Metod sistemin xətti hissəsinin aşağı keçirici filtr (filtr hipotezi) olması fərziyyəsinə əsaslanır. Sistemdəki öz-özünə salınmaların harmoniklərə yaxın ola biləcəyi şərtləri müəyyən edək. Biz özümüzü şəkildəki kimi sistemlərlə məhdudlaşdırırıq. 3 qeyri-xətti elementin və xətti hissənin ardıcıl əlaqəsinə endirilə bilər. İstinad siqnalının sabit bir dəyər olduğunu güman edirik, sadəlik üçün onu sıfıra bərabər götürəcəyik. Və səhv siqnalı (Şəkil 3) harmonikdir:

(1)

Qeyri-xətti elementin çıxış siqnalı, hər hansı bir dövri siqnal kimi - Şəkil 3-də bunlar düzbucaqlı salınımlardır - Furye seriyasının harmoniklərinin cəmi kimi təqdim edilə bilər.

Fərz edək ki, sistemin xətti hissəsi aşağı keçirici filtrdir (şəkil 4) və w 0 tezliyi ilə yalnız birinci harmonik keçir. 2w 0 və daha yüksək harmonik tezliyi olan ikincisi xətti hissə ilə süzülür. Bu halda, on xətti çıxış hissələri yalnız praktiki olaraq mövcud olacaqdır birinci harmonik , və daha yüksək harmoniklərin təsiri laqeyd qala bilər

Beləliklə, əgər sistemin xətti hissəsi aşağı keçirici filtrdirsə və öz-özünə salınma tezliyi w 0 şərtlərini ödəyirsə.

, (4)

Sistemin xətti hissəsinin aşağı keçirici filtr olduğu fərziyyəsi deyilir filtr hipotezi . Xətti hissənin köçürmə funksiyasının məxrəcinin və sayının çoxhədlilərinin dərəcələri arasındakı fərq olduqda filtr fərziyyəsi həmişə təmin edilir.

(5)

ən azı iki

Şərt (6) bir çox real sistemlər üçün qənaətbəxşdir. Buna misal olaraq ikinci dərəcəli aperiodik əlaqə və real inteqrasiyanı göstərmək olar

. (7)

Harmonikaya yaxın öz-özünə salınmaların öyrənilməsində qeyri-xətti elementin çıxışında yalnız dövri rəqslərin birinci harmonikası nəzərə alınır, çünki hər halda daha yüksək harmoniklər xətti hissə tərəfindən praktiki olaraq süzülür. Öz-özünə salınma rejimində, harmonik xəttiləşdirmə qeyri-xətti element. Qeyri-xətti element ilə ekvivalent xətti element ilə əvəz olunur kompleks qazanc giriş harmonik siqnalının amplitudasından asılı olaraq (funksiyanı təsvir edir):

-nin real və xəyali hissələri haradadır,

- mübahisə,

- modul.

Ümumi halda, bu, həm amplituda, həm də özünü salınımların tezliyindən və sabit komponentdən asılıdır. Fiziki cəhətdən mürəkkəb qeyri-xətti element qazancı, daha çox adlandırılır harmonik xəttiləşmə əmsalı , yeyin birinci harmonikdə qeyri-xətti elementin kompleks qazancı. Harmonik xəttiləşdirmə əmsalı modulu

(9)

qeyri-xətti elementin çıxışında birinci harmonikanın amplitudasının giriş harmonik siqnalının amplitudasına nisbətinə ədədi olaraq bərabərdir.

Arqument

(10)

çıxış rəqslərinin birinci harmonikası ilə giriş harmonik siqnalı arasında faza sürüşməsini xarakterizə edir. Tək qiymətli qeyri-xəttilər üçün, məsələn, Şəkil 1-də. 2a və 2b, həqiqi ifadə və

Birmənalı olmayan qeyri-xəttiliklər üçün şək. 2, c, 2, d, düsturla müəyyən edilir

burada S histerezis dövrəsinin sahəsidir. Əgər histerezis döngəsi müsbət istiqamətdə keçərsə (şəkil 2c), əks halda isə mənfi işarə ilə (şəkil 2d) S sahəsi artı işarəsi ilə götürülür.

Ümumi halda və düsturlarla hesablanır

, (12)

burada , qeyri-xətti funksiyadır (qeyri-xətti elementin xarakteristikası).

Yuxarıda deyilənləri nəzərə alaraq, harmonikə yaxın öz-özünə salınmaların tədqiqində qeyri-xətti ASR (şəkil 3) qeyri-xətti element əvəzinə harmonik xəttiləşmə əmsalı olan ekvivalentlə əvəz olunur (şək. 5). Şəkildəki qeyri-xətti elementin çıxış siqnalı. 5 kimi qeyd olunur, belədir

qeyri-xətti elementin yalnız əmələ gətirdiyini vurğulayır

vibrasiyaların ilk harmonikası. Tipik qeyri-xəttilər üçün harmonik xəttiləşdirmə əmsalları üçün düsturlar ədəbiyyatda tapıla bilər, məsələn. Əlavə B-dəki cədvəldə tədqiq olunan rele elementlərinin xüsusiyyətləri, formulları və onların hodoqrafları göstərilir. İfadə ilə təyin olunan harmonik xəttiləşdirmənin qarşılıqlı əmsalı üçün düsturlar və hodoqraflar da mövcuddur.

, (13)

-nin real və xəyali hissələri haradadır. Hodoqraflar və müvafiq olaraq , və koordinatlarında qurulur.

İndi öz-özünə salınmaların mövcudluğunun şərtlərini yazaq. Şəkildəki sistem. 5 xətti ilə bərabərdir. Xətti sistemdə sabitlik sərhədində olarsa, sönümsüz rəqslər olur. Nyquist meyarına uyğun olaraq sabitlik sərhədinin şərtindən istifadə edirik:

. (14)

Tənlik (14) yemək öz-özünə salınımların mövcudluğu şərti, harmonikə yaxındır. Əgər varsa əsl müsbət (14) tənliyinin A və w 0 həlləri, onda qeyri-xətti ASR-də harmoniklərə yaxın öz-özünə salınmalar var. Əks halda, öz-özünə salınımlar yoxdur və ya harmonik deyil. Tənlik (14) ikiyə bölünür - həqiqi və xəyali hissələrə görə:

;

(14) tənliyinin hər iki hissəsini (13) düsturuna bölmək və nəzərə almaqla, Goldfarb L.S. şəklində öz-özünə rəqslərin mövcudluğu şərtini əldə edirik:

. (17)

(17) tənliyi də ikiyə bölünür:

(18)

bəzi hallarda isə öz-özünə salınmaların parametrlərini təyin etmək üçün onlardan istifadə etmək daha rahatdır.

Qoldfarb sistemin (17) həlli və öz-özünə rəqslərin dayanıqlığının təyini üçün qrafik-analitik üsul təklif etmişdir.

Koordinatlarda , və , hodoqraflar və qurulur (şək. 6a). Hodoqraflar kəsişirsə, o zaman öz-özünə salınmalar mövcuddur. Öz-özünə salınmaların parametrləri - A və w 0 kəsişmə nöqtələrində müəyyən edilir - hodoqrafa görə tezlik w 0, hodoqrafa görə amplituda. Əncirdə. 6a – iki sərhəd dövrünün mövcudluğunu göstərən iki kəsişmə nöqtəsi.

Öz-özünə salınmaların dayanıqlığını müəyyən etmək üçün Qoldfarbın fikrincə, AFC boyu artan tezlik istiqamətində hərəkət edərkən xətti hissənin AFC-nin sol tərəfi lyuklanır (şəkil 6).

Əgər kəsişmə nöqtəsində qeyri-xətti elementin hodoqrafı A amplitudasının artması istiqamətində hərəkət edərkən kölgəsiz sahədən kölgəli sahəyə keçirsə, öz-özünə salınmalar sabitdir.

Keçid kölgəli bölgədən kölgəsiz bölgəyə baş verərsə, o zaman öz-özünə salınmalar sabit deyil.

Əncirdə. 6b, Şek. 2-də göstərilən iki limit dövrünə uyğun gələn faza portretini keyfiyyətcə təsvir edir. 6, a. Parametrlərlə kəsişmə nöqtəsi və şək. 6a Şəkildəki qeyri-sabit limit dövrünə uyğundur. 6, b, parametrləri olan bir nöqtəyə və və öz-özünə salınımların parçalanmasına nail olmaq üçün , bu halda, hodoqraflar və kəsişməyin. Eyni təsirə ölü zonanın artırılması və ya B relesinin çıxış siqnalının amplitudasının azaldılması ilə nail olmaq olar. Xətti hissənin AFC-nin toxunduğu müəyyən bir limit dəyəri K l var. Səhv! Rabitə xətası. harada , amplitudanın qiyməti isə . Təbii ki, bu, sistemin faza portretinin keyfiyyətcə dəyişməsinə gətirib çıxarır.

ekosistemlər

Zoologiya

Biologiya

Uzun 19-cu əsr

yaxın tarix

Orta əsrlər

yeni vaxt

Müharibələrarası dövr