Приведенные к настоящему моменту в открытом банке задач ЕГЭ по математике (mathege.ru), решение которых основано на одной лишь формуле, представляющей собой классическое определение вероятности.

Понять формулу проще всего на примерах.
Пример 1. В корзине 9 красных шаров и 3 синих. Шары различаются только цветом. Наугад (не глядя) достаём один из них. Какова вероятность того, что выбранный таким образом шар окажется синего цвета?

Комментарий. В задачах по теории вероятности происходит нечто (в данном случае наше действие по вытаскиванию шара), что может иметь разный результат - исход. Нужно заметить, что на результат можно смотреть по-разному. "Мы вытащили какой-то шар" - тоже результат. "Мы вытащили синий шар" - результат. "Мы вытащили именно вот этот шар из всех возможных шаров" - такой наименее обобщенный взгляд на результат называется элементарным исходом. Именно элементарные исходы имеются в виду в формуле для вычисления вероятности.

Решение. Теперь вычислим вероятность выбора синего шара.
Событие А: "выбранный шар оказался синего цвета"
Общее число всех возможных исходов: 9+3=12 (количество всех шаров, которые мы могли бы вытащить)
Число благоприятных для события А исходов: 3 (количество таких исходов, при которых событие А произошло, - то есть, количество синих шаров)
P(A)=3/12=1/4=0,25
Ответ: 0,25

Посчитаем для той же задачи вероятность выбора красного шара.
Общее число возможных исходов останется тем же, 12. Число благоприятных исходов: 9. Искомая вероятность: 9/12=3/4=0,75

Вероятность любого события всегда лежит в пределах от 0 до 1.
Иногда в повседневной речи (но не в теории вероятности!) вероятность событий оценивают в процентах. Переход между математической и разговорной оценкой осуществляется путем умножения (или деления) на 100%.
Итак,
При этом вероятность равна нулю у событий, которые не могут произойти - невероятны. Например, в нашем примере это была бы вероятность вытащить из корзины зеленый шар. (Число благоприятных исходов равно 0, Р(А)=0/12=0, если считать по формуле)
Вероятность 1 имеют события, которые абсолютно точно произойдут, без вариантов. Например, вероятность того, что «выбранный шар окажется или красным или синим» - для нашей задачи. (Число благоприятных исходов: 12, Р(А)=12/12=1)

Мы рассмотрели классический пример, иллюстрирующий определение вероятности. Все подобные задачи ЕГЭ по теории вероятности решаются применением данной формулы.
На месте красных и синих шаров могут быть яблоки и груши, мальчики и девочки, выученные и невыученные билеты, билеты, содержащие и не содержащие вопрос по какой-то теме (прототипы , ), бракованные и качественные сумки или садовые насосы (прототипы , ) – принцип остается тем же.

Немного отличаются формулировкой задачи теории вероятности ЕГЭ, где нужно вычислить вероятность выпадения какого-то события на определенный день. ( , ) Как и в предыдущих задачах нужно определить, что является элементарным исходом, после чего применить ту же формулу.

Пример 2. Конференция длится три дня. В первый и второй день выступают по 15 докладчиков, в третий день – 20. Какова вероятность того, что доклад профессора М. выпадет на третий день, если порядок докладов определяется жеребьевкой?

Что здесь является элементарным исходом? – Присвоение докладу профессора какого-то одного из всех возможных порядковых номеров для выступления. В жеребьевке участвует 15+15+20=50 человек. Таким образом, доклад профессора М. может получить один из 50 номеров. Значит, и элементарных исходов всего 50.
А какие исходы благоприятные? – Те, при которых окажется, что профессор будет выступать в третий день. То есть, последние 20 номеров.
По формуле вероятность P(A)= 20/50=2/5=4/10=0,4
Ответ: 0,4

Жеребьевка здесь представляет собой установление случайного соответствия между людьми и упорядоченными местами. В примере 2 установление соответствия рассматривалось с точки зрения того, какое из мест мог бы занять конкретный человек. Можно к той же ситуации подходить с другой стороны: кто из людей с какой вероятностью мог бы попасть на конкретное место (прототипы , , , ):

Пример 3. В жеребьевке участвуют 5 немцев, 8 французов и 3 эстонца. Какова вероятность того, что первым (/вторым/седьмым/последним – не важно) будет выступать француз.

Количество элементарных исходов – количество всех возможных людей, которые могли бы по жеребьевке попасть на данное место. 5+8+3=16 человек.
Благоприятные исходы – французы. 8 человек.
Искомая вероятность: 8/16=1/2=0,5
Ответ: 0,5

Немного отличается прототип . Остались задачи про монеты () и игральные кости (), несколько более творческие. Решение этих задач можно посмотреть на страницах прототипов.

Приведем несколько примеров на бросание монеты или кубика.

Пример 4. Когда подбрасываем монету, какова вероятность выпадения решки?
Исходов 2 – орел или решка. (считается, что монета никогда не падает на ребро) Благоприятный исход – решка, 1.
Вероятность 1/2=0,5
Ответ: 0,5.

Пример 5. А если подбрасываем монету два раза? Какова вероятность того, что оба раза выпадет орел?
Главное определить, какие элементарные исходы будем рассматривать при подбрасывании двух монет. После подбрасывания двух монет может получиться один из следующих результатов:
1) PP – оба раза выпала решка
2) PO – первый раз решка, второй раз орел
3) OP – первый раз орел, второй раз решка
4) OO – оба раза выпал орел
Других вариантов нет. Значит, элементарных исходов 4. Благоприятный из них только первый, 1.
Вероятность: 1/4=0,25
Ответ: 0,25

Какова вероятность того, что из двух подбрасываний монеты один раз выпадет решка?
Количество элементарных исходов то же, 4. Благоприятные исходы – второй и третий, 2.
Вероятность выпадения одной решки: 2/4=0,5

В таких задачах может пригодиться ещё одна формула.
Если при одном бросании монеты возможных вариантов результата у нас 2, то для двух бросаний результатов будет 2·2=2 2 =4 (как в примере 5), для трех бросаний 2·2·2=2 3 =8, для четырех: 2·2·2·2=2 4 =16, … для N бросаний возможных результатов будет 2·2·...·2=2 N .

Так, можно найти вероятность выпадения 5 решек из 5 бросаний монеты.
Общее число элементарных исходов: 2 5 =32.
Благоприятных исходов: 1. (РРРРР – все 5 раз решка)
Вероятность: 1/32=0,03125

То же верно и для игральной кости. При одном бросании возможных результатов здесь 6. Значит, для двух бросаний: 6·6=36, для трех 6·6·6=216, и т. д.

Пример 6. Бросаем игральную кость. Какова вероятность, что выпадет четное число?

Всего исходов: 6, по числу граней.
Благоприятных: 3 исхода. (2, 4, 6)
Вероятность: 3/6=0,5

Пример 7. Бросаем две игральные кости. Какова вероятность, что в сумме выпадет 10? (округлить до сотых)

Для одного кубика 6 возможных исходов. Значит, для двух, по вышеупомянутому правилу, 6·6=36.
Какие исходы будут благоприятными для того, чтоб в сумме выпало 10?
10 надо разложить на сумму двух чисел от 1 до 6. Это можно сделать двумя способами: 10=6+4 и 10=5+5. Значит, для кубиков возможны варианты:
(6 на первом и 4 на втором)
(4 на первом и 6 на втором)
(5 на первом и 5 на втором)
Итого, 3 варианта. Искомая вероятность: 3/36=1/12=0,08
Ответ: 0,08

Другие типы задач B6 будут рассмотрены в одной из следующих статей «Как решать».

Задание

Вариант демо

1. и - независимые события. Тогда справедливо следующее утверждение: а) они являются взаимоисключающими событиями

б)

г)

д)

2. , , - вероятности событий , , 0 " style="margin-left:55.05pt;border-collapse:collapse;border:none">

3. Вероятности событий и https://pandia.ru/text/78/195/images/image012_30.gif" width="105" height="28 src=">.gif" width="55" height="24"> есть:

а) 1,25 б)0,3886 в)0,25 г)0,8614

д) нет правильного ответа

4. Докажите равенство с помощью таблиц истинности или покажите, что оно неверно.

Раздел 2. Вероятности объединения и пересечения событий, условная вероятность, формулы полной вероятности и Байеса.

Задание : выберите правильный ответ и отметьте в таблице соответствующую букву.

Вариант демо

1. Бросаем одновременно две игральные кости. Какова вероятность, что сумма выпавших очков не больше 6?

а) ; б) ; в) ; г) ;

д) нет правильного ответа

2. Каждая буква слова «РЕМЕСЛО» написана на отдельной карточке, затем карточки перемешаны. Вынимаем три карточки наугад. Какова вероятность получить слово «ЛЕС»?

а) ; б) ; в) ; г) ;

д) нет правильного ответа

3. Среди студентов второго курса 50% ни разу не пропускали занятия, 40% пропускали занятия не более 5 дней за семестр и 10% пропускали занятия 6 и более дней. Среди студентов, не пропускавших занятия, 40% получили высший балл, среди тех, кто пропустил не больше 5 дней – 30% и среди оставшихся – 10% получили высший балл. Студент получил на экзамене высший балл. Найти вероятность того, что он пропускал занятия более 6 дней.

а) https://pandia.ru/text/78/195/images/image024_14.gif" width="17 height=53" height="53">; в) ; г) ; д) нет правильного ответа

Тест по курсу теории вероятностей и математической статистики.

Раздел 3. Дискретные случайные величины и их числовые характеристики.

Задание : выберите правильный ответ и отметьте в таблице соответствующую букву.

Вариант демо

1 . Дискретные случайные величины X и Y заданы своими законами

распределения

Случайная величина Z = X+Y. Найти вероятность

а) 0.7; б) 0.84; в) 0.65; г) 0.78; д) нет правильного ответа

2. X, Y, Z – независимые дискретные случайные величины. Величина X распределена по биномиальному закону с параметрами n=20 и p=0.1. Величина Y распределена по геометрическому закону с параметром p=0.4. Величина Z распределена по закону Пуассона с параметром =2. Найти дисперсию случайной величины U= 3X+4Y-2Z

а) 16.4 б) 68.2; в) 97.3; г) 84.2; д) нет правильного ответа

3. Двумерный случайный вектор (X, Y) задан законом распределения

Событие , событие . Какова вероятность события А+В?

а) 0.62; б) 0.44; в) 0.72; г) 0.58; д) нет правильного ответа

Тест по курсу теории вероятностей и математической статистики.

Раздел 4. Непрерывные случайные величины и их числовые характеристики.

Задание : выберите правильный ответ и отметьте в таблице соответствующую букву.

Вариант демо

1. Независимые непрерывные случайные величины X и Y равномерно распределены на отрезках: X на https://pandia.ru/text/78/195/images/image032_6.gif" width="32" height="23">.

Случайная величина Z = 3X +3Y +2. Найти D(Z)

а) 47.75; б) 45.75; в) 15.25; г) 17.25; д) нет правильного ответа

2 ..gif" width="97" height="23">

а) 0.5; б) 1; в) 0; г) 0.75; д) нет правильного ответа

3. Непрерывная случайная величина X задана своей плотностью вероятности https://pandia.ru/text/78/195/images/image036_7.gif" width="99" height="23 src=">.

а) 0.125; б) 0.875; в)0.625; г) 0.5; д) нет правильного ответа

4. Случайная величина X распределена нормально с параметрами 8 и 3. Найти

а) 0.212; б) 0.1295; в)0.3413; г) 0.625; д) нет правильного ответа

Тест по курсу теории вероятностей и математической статистики.

Раздел 5. Введение в математическую статистику.

Задание : выберите правильный ответ и отметьте в таблице соответствующую букву.

Вариант демо

1. Предлагаются следующие оценки математического ожидания https://pandia.ru/text/78/195/images/image041_6.gif" width="98" height="22">:

А) https://pandia.ru/text/78/195/images/image043_5.gif" width="205" height="40">

В) https://pandia.ru/text/78/195/images/image045_4.gif" width="205" height="40">

Д) 0 " style="margin-left:69.2pt;border-collapse:collapse;border:none">

2. Дисперсия каждого измерения в предыдущей задаче есть . Тогда наиболее эффективной из полученных в первой задаче несмещенных оценок будет оценка

3. На основании результатов независимых наблюдений случайной величины X, подчиняющейся закону Пуассона, построить методом моментов оценку неизвестного параметра 425 " style="width:318.65pt;margin-left:154.25pt;border-collapse:collapse; border:none">

а) 2.77; б) 2.90; в) 0.34; г) 0.682; д) нет правильного ответа

4. Полуширина 90% доверительного интервала, построенного для оценки неизвестного математического ожидания нормально распределенной случайной величины X для объема выборки n=120, выборочного среднего https://pandia.ru/text/78/195/images/image052_3.gif" width="19" height="16">=5, есть

а) 0.89; б) 0.49 ; в) 0.75; г) 0.98; д) нет правильного ответа

Матрица проверки – тест демо

Раздел 1
		А -	Б +	В -	Г -	Д +
Раздел 2
Раздел 3.
Раздел 4
Раздел 5

Вариант 1.

Под случайным событием, связанным с некоторым опытом, понимается всякое событие, которое при осуществлении этого опыта

а) не может произойти;

б) либо происходит, либо нет;

в) обязательно произойдет.

Если событие А происходит тогда и только тогда, когда происходит событие В , то их называют

а) равносильными;

б) совместными;

в) одновременными;

г) тождественными.

Если полная система состоит из 2-х несовместных событий, то такие события называются

а) противоположными;

б) несовместными;

в) невозможными;

г) равносильными.

А 1 – появление четного числа очков. Событие А 2 - появление 2-х очков. Событие А 1  А 2 состоит в том, что выпало

а) 2; б) 4; в) 6; г) 5.

Вероятность достоверного события равна

а) 0; б) 1; в) 2; г) 3.

Вероятность произведения двух зависимых событий А и В вычисляется по формуле

а) Р(А В) = Р(А) Р(В); б) Р(А В) = Р(А)+Р(В) – Р(А) Р(В);

в) Р(А В) = Р(А)+Р(В) + Р(А) Р(В); г) Р(А В) = Р(А) Р(А | В).

Из 25 экзаменационных билетов, занумерованных числами от 1 до 25, студент наудачу извлекает 1. Какова вероятность того, что студент сдаст экзамен, если он знает ответы на 23 билета?

а) ; б) ; в) ; г) .

В коробке 10 шаров: 3 белых, 4 черных, 3 синих. Наудачу вытащили 1 шарик. Какова вероятность, что он будет либо белым, либо черным?

а) ; б) ; в) ; г) .

Имеется 2 ящика. В первом 5 стандартных и 1 нестандартная деталь. Во втором 8 стандартных и 2 нестандартные детали. Из каждого ящика наудачу вынимают по одной детали. Какова вероятность того, что вынутые детали окажутся стандартными?

а) ; б) ; в) ; г) .

Из слова «математика » выбирается наугад одна буква. Какова вероятность того, что эта буква «а »?

а) б) ; в) ; г) .

Вариант 4.

Если событие в данном опыте не может произойти, то оно называется

а) невозможным;

б) несовместным;

в) необязательным;

г) недостоверным.

Опыт с подбрасыванием игральной кости. Событие А выпадает число очков не большее 3. Событие В выпадает четное число очков. Событие А  В состоит в том, что выпала грань с номером

а) 1; б) 2; в) 3; г) 4.

События, образующие полную систему попарно несовместных и равновероятных событий называются

а) элементарными;

б) несовместными;

в) невозможными;

г) достоверными.

а) 0; б) 1; в) 2; г) 3.

В магазин поступило 30 холодильников. 5 из них имеют заводской дефект. Случайным образом выбирается один холодильник. Какова вероятность, что он будет без дефекта?

а) ; б); в) ; г) .

Вероятность произведения двух независимых событий А и В вычисляется по формуле

а) Р(А В) = Р(А) Р(В | А); б) Р(А В) = Р(А) + Р(В) – Р(А) Р(В);

в) Р(А В) = Р(А) + Р(В) + Р(А) Р(В); г) Р(А В) = Р(А) Р(В).

В классе 20 человек. Из них 5 отличников, 9 хорошистов, 3 имеют тройки и 3 имеют двойки. Какова вероятность того, что выбранный случайно ученик либо хорошист, либо отличник?

а) ; б) ; в) ; г) .

9. В первой коробке 2 белых и 3 черных шара. Во второй коробке 4 белых и 5 черных шаров. Наудачу извлекают из каждой коробке по одному шару. Какова вероятность того, что оба шара окажутся белыми?

а) ; б) ; в) ; г) .

10. Вероятность достоверного события равна

а) 0; б) 1; в) 2; г) 3.

Вариант 3.

Если в данном опыте никакие два из событий не могут произойти одновременно, то такие события называются

а) несовместными;

б) невозможными;

в) равносильными;

г) совместными.

Совокупность несовместных событий таких, что в результате опыта должно произойти хотя бы одно из них называются

а) неполной системой событий; б) полной системой событий;

в) целостной системой событий; г) не целостной системой событий.

Произведением событий А 1 и А 2

а) происходит событие А 1 , событие А 2 не происходит;

б) происходит событие А 2 , событие А 1 не происходит;

в) события А 1 и А 2 происходят одновременно.

В партии из 100 деталей 3 бракованных. Какова вероятность того, что взятая наудачу деталь окажется бракованной?

а)
; б) ; в)
;
.

Сумма вероятностей событий образующих полную систему равна

а) 0; б) 1; в) 2; г) 3.

Вероятность невозможного события равна

а) 0; б) 1; в) 2; г) 3.

А и В вычисляется по формуле

а) Р(А+В) = Р(А) + Р(В); б) Р(А+В) = Р(А) + Р(В) – Р(А В);

в) Р(А+В) = Р(А) + Р(В) + Р(А В); г) Р(А+В) = Р(А В) – Р(А) + Р(В).

На полке в произвольном порядке расставлено 10 учебников. Из них 1 по математике, 2 по химии, 3 по биологии и 4 по географии. Студент произвольно взял 1 учебник. Какова вероятность того, что он будет либо по математике, либо по химии?

а) ; б) ; в) ; г) .

а) несовместными;

б) независимыми;

в) невозможными;

г) зависимыми.

В двух коробках находятся карандаши одинаковой величины и формы. В первой коробке: 5 красных, 2 синих и 1 черный карандаш. Во второй коробке: 3 красных, 1 синий и 2 желтых. Наудачу извлекают по одному карандашу из каждой коробки. Какова вероятность того, что оба карандаша будут синими?

а) ; б) ; в) ; г) .

Вариант 2.

Если событие происходит в данном опыте обязательно, то оно называется

а) совместным;

б) реальным;

в) достоверным;

г) невозможным.

Если появление одного из событий не исключает появление другого в одном и том же испытании, то такие события называются

а) совместными;

б) несовместными;

в) зависимыми;

г) независимыми.

Если наступление события В не оказывает ни какого влияния на вероятность наступления события А, и наоборот, наступление события А не оказывает ни какого влияния на вероятность наступления события В, то события А и В называются

а) несовместными;

б) независимыми;

в) невозможными;

г) зависимыми.

Суммой событий А 1 и А 2 называется событие, которое осуществляется в том случае, когда

а) происходит хотя бы одно из событий А 1 или А 2 ;

б) события А 1 и А 2 не происходят;

в) события А 1 и А 2 происходят одновременно.

Вероятность любого события есть неотрицательное число, не превосходящее

а) 1; б) 2; в) 3; г) 4.

Из слова «автоматика » выбирается наугад одна буква. Какова вероятность того, что это будет буква «а »?

а) ; б) ; в) ; г) .

Вероятность суммы двух несовместных событий А и В вычисляется по формуле

а) Р(А+В) = Р(А) + Р(В); б) Р(А+В) = Р(А В) – Р(А) + Р(В);

в) Р(А+В) = Р(А) + Р(В) + Р(А В); г) Р(А+В) = Р(А) + Р(В) – Р(А В).

В первой коробке 2 белых и 5 черных шаров. Во второй коробке 2 белых и 3 черных шара. Из каждой коробки наудачу вынули по 1 шару. Какова вероятность, что оба шара окажутся черными?

а) ; б) ; в) ; г) .

1. МАТЕМАТИЧЕСКАЯ НАУКА, УСТАНАВЛИВАЮЩАЯ ЗАКОНОМЕРНОСТИ СЛУЧАЙНЫХ ЯВЛЕНИЙ ЭТО:

а) медицинская статистика

б) теория вероятностей

в) медицинская демография

г) высшая математика

Правильный ответ: б

2. ВОЗМОЖНОСТЬ РЕАЛИЗАЦИИ КАКОГО-ЛИБО СОБЫТИЯ ЭТО:

а) эксперимент

б) схема случаев

в) закономерность

г) вероятность

Правильный ответ г

3. ЭКСПЕРИМЕНТ ЭТО:

а) процесс накопления эмпирических знаний

б) процесс измерения или наблюдения за действием с целью сбора данных

в) изучение с охватом всей генеральной совокупности единиц наблюдения

г) математическое моделирование процессов реальности

Правильный ответ б

4. ПОД ИСХОДОМ В ТЕОРИИ ВЕРОЯТНОСТИ ПОНИМАЮТ:

а) неопределенный результат эксперимента

б) определенный результат эксперимента

в) динамику вероятностного процесса

г) отношение числа единиц наблюдения к генеральной совокупности

Правильный ответ б

5. ВЫБОРОЧНОЕ ПРОСТРАНСТВО В ТЕОРИИ ВЕРОЯТНОСТИ ЭТО:

а) структура явления

б) все возможные исходы.эксперимента

в) соотношение между двумя самостоятельными совокупностями

г) соотношение между двумя зависимыми совокупностями

Правильный ответ б

6. ФАКТ, КОТОРЫЙ ПРИ РЕАЛИЗАЦИИ ОПРЕДЕЛЕННОГО КОМПЛЕКСА УСЛОВИЙ МОЖЕТ ПРОИЗОЙТИ ИЛИ НЕ ПРОИЗОЙТИ:

а) частота встречаемости

б) вероятность

в) явление

г) событие

Правильный ответ г

7. СОБЫТИЯ, КОТОРЫЕ ПРОИСХОДЯТ С ОДИНАКОВОЙ ЧАСТОТОЙ,И НИ ОДНО ИЗ НИХ НЕ ЯВЛЯЕТСЯ ОБЪЕКТИВНО БОЛЕЕ ВОЗМОЖНЫМ, ЧЕМ ДРУГИЕ:

а) случайные

б) равновероятные

в) равнозначные

г) выборочные

Правильный ответ б

8. СОБЫТИЕ, КОТОРОЕ ПРИ РЕАЛИЗАЦИИ ОПРЕДЕЛЕННЫХ УСЛОВИЙ ПРОИЗОЙДЕТ НЕПРЕМЕННО, СЧИТАЕТСЯ:

а) нужным

б) ожидаемым

в) достоверным

г) приоритетным

Правильный ответ в

8. ПРОТИВОПОЛОЖНОСТЬЮ ПО ОТНОШЕНИЮ К ДОСТОВЕРНОМУ СОБЫТИЮ ЯВЛЯЕТСЯ СОБЫТИЕ:

а) ненужное

б) неожиданное

в) невозможное

г) неприоритетное

Правильный ответ в

10. ВЕРОЯТНОСТЬ ПОЯВЛЕНИЯ СЛУЧАЙНОГО СОБЫТИЯ:

а) больше нуля и меньше единицы

б) больше единицы

в) меньше нуля

г) представлена целыми числами

Правильный ответ а

11. СОБЫТИЯ ОБРАЗУЮТ ПОЛНУЮ ГРУППУ СОБЫТИЙ, ЕСЛИПРИ РЕАЛИЗАЦИИ ОПРЕДЕЛЕННЫХ УСЛОВИЙ, ХОТЯ БЫ ОДНО ИЗ НИХ:

а) появится непременно

б) появится в 90% экспериментов

в) появится в 95% экспериментов

г) появится в 99% экспериментов

Правильный ответ а

12. ВЕРОЯТНОСТЬ ПОЯВЛЕНИЯ КАКОГО-ЛИБО СОБЫТИЯ ИЗ ПОЛНОЙ ГРУППЫ СОБЫТИЙ ПРИ РЕАЛИЗАЦИИ ОПРЕДЕЛЕННЫХ УСЛОВИЙ РАВНА:

Правильный ответ г

13. ЕСЛИ НИКАКИЕ ДВА СОБЫТИЯ ПРИ РЕАЛИЗАЦИИ ОПРЕДЕЛЕННЫХ УСЛОВИЙ НЕ МОГУТ ПОЯВИТЬСЯ ОДНОВРЕМЕННО, ТО ОНИ НАЗЫВАЮТСЯ:

а) достоверными

б) несовместными

в) случайные

г) вероятные

Правильный ответ б

14. ЕСЛИ ПРИ РЕАЛИЗАЦИИ ОПРЕДЕЛЕННЫХ УСЛОВИЙ НИ ОДНО ИЗ ОЦЕНИВАЕМЫХ СОБЫТИЙ НЕ ЯВЛЯЕТСЯ ОБЪЕКТИВНО БОЛЕЕ ВОЗМОЖНЫМ, ЧЕМ ДРУГИЕ, ТО ОНИ:

а) равноправные

б) совместные

в) равновозможные

г) несовместимые

Правильный ответ в

15. ВЕЛИЧИНА, КОТОРАЯ ПРИ РЕАЛИЗАЦИИ ОПРЕДЕЛЕННЫХ УСЛОВИЙ МОЖЕТ ПРИНИМАТЬ РАЗЛИЧНЫЕ ЗНАЧЕНИЯ, НАЗЫВАЕТСЯ:

а) случайной

б) равновозможной

в) выборочной

г) суммарной

Правильный ответ а

16. ЕСЛИ НАМ ИЗВЕСТНО КОЛИЧЕСТВО ВОЗМОЖНЫХ ИСХОДОВ НЕКОТОРОГО СОБЫТИЯ И ОБЩЕЕ КОЛИЧЕСТВО ИСХОДОВ В ВЫБОРОЧНОМ ПРОСТРАНСТВЕ, ТО МОЖНО РАССЧИТАТЬ:

а) условную вероятность

б) классическую вероятность

в) эмпирическую вероятность

г) субъективную вероятность

Правильный ответ б

17. КОГДА МЫ НЕ ОБЛАДАЕМ ДОСТАТОЧНОЙ ИНФОРМАЦИЕЙ О ПРОИСХОДЯЩЕМ И НЕ МОЖЕМ ОПРЕДЕЛИТЬ ЧИСЛО ВОЗМОЖНЫХ ИСХОДОВ ИНТЕРЕСУЮЩЕГО НАС СОБЫТИЯ,МЫ МОЖЕМ РАССЧИТАТЬ:

а) условную вероятность

б) классическую вероятность

в) эмпирическую вероятность

г) субъективную вероятность

Правильный ответ в

18. ОСНОВЫВАЯСЬ НА ВАШИХ ЛИЧНЫХ НАБЛЮДЕНИЯХ ВЫ ОПЕРИРУЕТЕ:

а) объективной вероятностью

б) классической вероятностью

в) эмпирической вероятностью

г) субъективной вероятностью

Правильный ответ г

19. СУММОЙ ДВУХ СОБЫТИЙ А И В НАЗЫВАЕТСЯ СОБЫТИЕ:

а) состоящее в последовательном появлении или события А, или события В, исключая совместное их появление

б) состоящее в появлении или события А, или события В

в) состоящее в появлении или события А, или события В, или событий А и В вместе

г) состоящее в появлении события А и события В совместно

Правильный ответ в

20. ПРОИЗВЕДЕНИЕМ ДВУХ СОБЫТИЙ А И В ЯВЛЯЕТСЯ СОБЫТИЕ, ЗАКЛЮЧАЮЩЕЕСЯ В:

а) совместном появлении событий А и В

б) последовательном появлении событий А и В

в) появлении или события А, или события В, или событий А и В вместе

г) появлении или события А, или события В

Правильный ответ а

21. ЕСЛИ СОБЫТИЕ А НЕ ВЛИЯЕТ НА ВЕРОЯТНОСТЬ ПОЯВЛЕНИЯ СОБЫТИЯ В , И НАОБОРОТ, ТОИХ МОЖНО СЧИТАТЬ:

а) независимыми

б) разгруппированными

в) дистанционными

г) разнородными

Правильный ответ а

22. ЕСЛИ СОБЫТИЕ А ВЛИЯЕТ НА ВЕРОЯТНОСТЬ ПОЯВЛЕНИЯ СОБЫТИЯ В, И НАОБОРОТ, ТОИХ МОЖНО СЧИТАТЬ:

а) однородными

б) сгруппированными

в) одномоментными

г) зависимыми

Правильный ответ г

23. ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ:

а) вероятность суммы двух совместных событий равняется сумме вероятностей этих событий

б) вероятность последовательного появления двух совместных событий равняется сумме вероятностей этих событий

в) вероятность суммы двух несовместных событий равняется сумме вероятностей этих событий

г) вероятность непоявления двух несовместных событий равняется сумме вероятностей этих событий

Правильный ответ в

24.СОГЛАСНО ЗАКОНУ БОЛЬШИХ ЧИСЕЛ, КОГДА ЭКСПЕРИМЕНТ ПРОВОДИТСЯ БОЛЬШОЕ ЧИСЛО РАЗ:

а) эмпирическая вероятность стремится к классической

б) эмпирическая вероятность удаляется от классической

в) субъективная вероятность превышает классическую

г) эмпирическая вероятность не меняется по отношению к классической

Правильный ответ а

25. ВЕРОЯТНОСТЬ ПРОИЗВЕДЕНИЯ ДВУХ СОБЫТИЙ А И В РАВНА ПРОИЗВЕДЕНИЮ ВЕРОЯТНОСТИ ОДНОГО ИЗ НИХ (А) НА УСЛОВНУЮ ВЕРОЯТНОСТЬ ДРУГОГО (В) , ВЫЧИСЛЕННУЮ ПРИ УСЛОВИИ, ЧТО ПЕРВОЕ ИМЕЛО МЕСТО:

а) теорема умножения вероятностей

б) теорема сложения вероятностей

в) теорема Байеса

г) теорема Бернулли

Правильный ответ а

26. ОДНО ИЗ СЛЕДСТВИЙ ТЕОРЕМЫ УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ:

б) если событие А влияет на событие В, то и событие В влияет на событие А

г) если событие Ане влияет на событие В, то и событие В не влияет на событие А

Правильный ответ в

27. ОДНО ИЗ СЛЕДСТВИЙ ТЕОРЕМЫ УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ:

а) если событие А зависит от события В, то и событие В зависит от события А

б) вероятность произведения независимых событий равна произведению вероятностей этих событий

в) если событие А не зависит от события В, то и событие В не зависит от события А

г) вероятность произведения зависимых событий равна произведению вероятностей этих событий

Правильный ответ б

28. ПЕРВОНАЧАЛЬНЫЕ ВЕРОЯТНОСТИ ГИПОТЕЗ ДО ПОЛУЧЕНИЯ ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИИ, НАЗЫВАЮТСЯ

а) априорными

б) апостериорными

в) предварительными

г) начальными

Правильный ответ а

29. ВЕРОЯТНОСТИ, ПЕРЕСМОТРЕННЫЕ ПОСЛЕ ПОЛУЧЕНИЯ ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИИ, НАЗЫВАЮТСЯ

а) априорными

б) апостериорными

в) предварительными

г) окончательными

Правильный ответ б

30. КАКАЯ ТЕОРЕМА ТЕОРИИ ВЕРОЯТНОСТИ МОЖЕТ ПРИМЕНЯТЬСЯ ПРИ ПОСТАНОВКЕ ДИАГНОЗА

а) Бернулли

б) Байеса

в) Чебышева

г) Пуассона

Правильныйответ б

А) !

Б)

B)

Г) P(A)=

Порядок не важен при использовании

А) размещений

Б) перестановок

В) сочетаний

Г) перестановок и размещений

А) 12131415=32760

Б) 131415=2730

В) 121314=2184

Г) 1415=210

Сочетание из n элементов по m -это

А) число подмножеств, содержащих m элементов

Б) количество изменений места элементом данного множества

В) количество способов выбора m элементов из n c учетом порядка

Г) количество способов выбора m элементов из n без учета порядка

Сколько существует способов, чтобы рассадить квартет из одноименной басни И.А.Крылова?

А) 24

Б) 4

В) 8

Г) 6

Сколькими способами можно выбрать в группе из 30 человек одного старосту и одного физорга?

А) 30

Б) 870

В) 435

Г) 30!

А)

Б)

В)

Г)

А)

Б) (m-2)(m-1)m

B) (m-1)m

Г) (m-2)(m-1)

Сколькими способами можно в группе из 30 человек послать 5 человек участвовать в колледжном пробеге?

А) 17100720

Б) 142506

В) 120

Г) 30!

Восемь студентов обменялись рукопожатиями. Сколько было рукопожатий?

А) 40320

Б) 28

В) 16

Г) 64

Сколькими способами можно выбрать 3 книги из 9 предложенных?

А)

Б)

В) Р 9

Г) 3Р 9

В вазе 5 красных и 3 белых розы. Сколькими способами можно взять 4 цветка?

А)

Б)

В)

Г)

В вазе 8 красных и 3 белых розы. Сколькими способами можно взять 2 красных и 1белую розы?

А)

Б)

В)

Г)

А) 110

Б) 108

В) -12

Г) 9

В почтовом ящике 38 отделений. Сколькими способами можно положить в ящик 35 одинаковых открыток так, чтобы в каждом ящике было не более одной открытки?

А)

Б) 35!

В)

Г) 38!

Сколько различных перестановок можно образовать из слова «слон»?

А) 6

Б) 4

В) 24

Г) 8

Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?

А) 10!

Б) 90

В) 45

Г) 100

Сколько различных двузначных чисел можно образовать из цифр 1,2,3,4?

А) 16

Б) 24

В) 12

Г) 6

На 5 сотрудников выделены 3 путевки. Сколькими способами их можно распределить, если все путевки различны?

А) 10

Б) 60

В) 125

Г) 243

А) (6;+)

Б) (-;6)

В) (0; +)

Г) (0;6)

А)

Б)

В)

Г)

А) 4

Б) 3

В) 2

Г) 5

Записать формулой фразу «число сочетаний из n элементов по 3 в 5 раз меньше числа сочетаний из n +2 элементов по 4 »

А)

Б)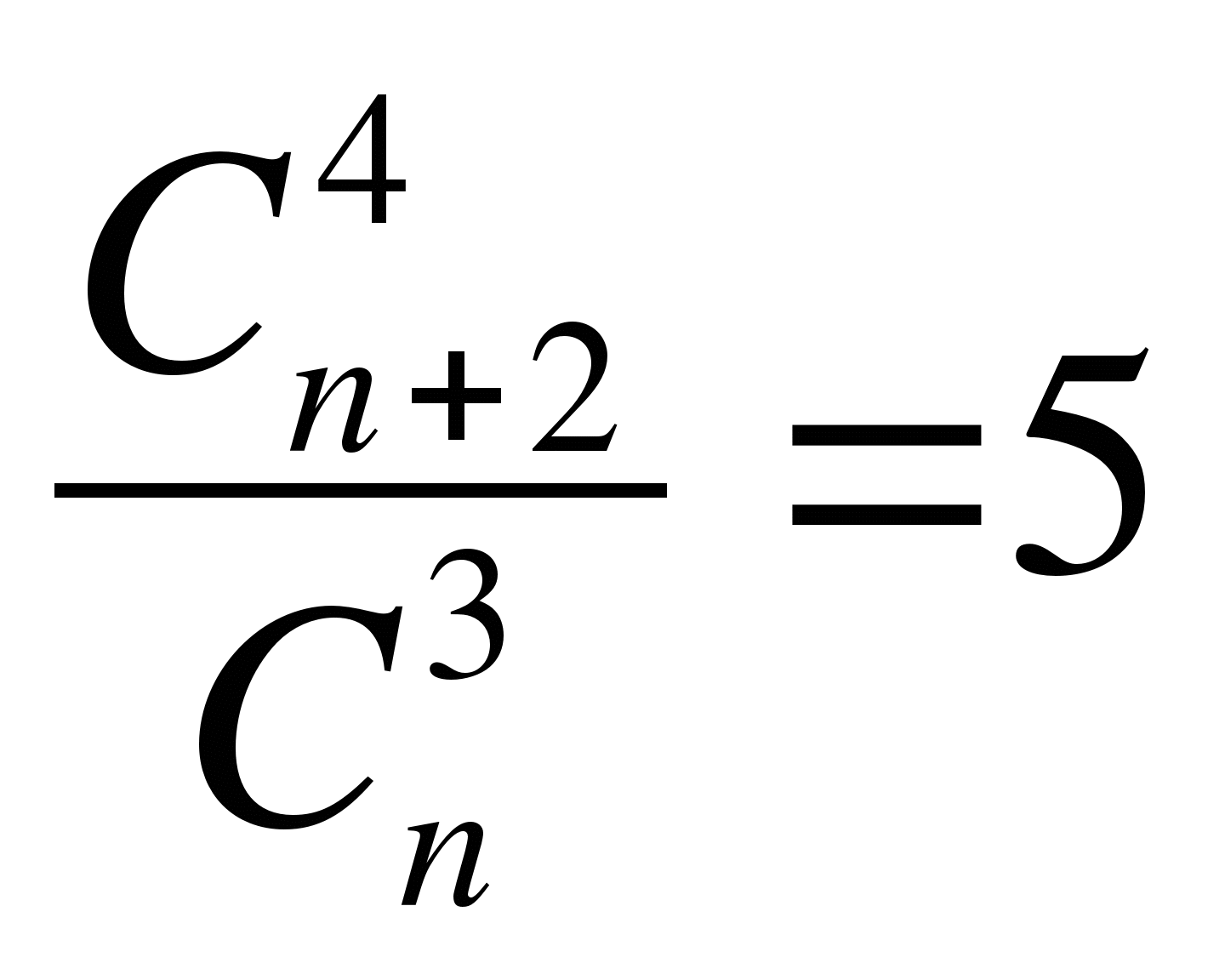

В)

Г)

Сколькими способами можно рассадить 28 студентов в лекционном зале?

А) 2880

Б) 5600

В) 28!

Г) 7200

Сколькими способами из 25 рабочих можно составить бригады по 5 человек в каждой?

А) 25!

Б)

В)

Г) 125

В группе 26 студентов. Сколькими способами можно выделить 2 человека для дежурства так, чтобы один из них был старшим?

А)

Б)

В) 24!

Г) 52

А) 6

Б) 5

В)

Г) 15

Сколько пятизначных чисел можно составить из цифр 1,2,3,4,5 без повторений?

А) 24

Б) 6

В) 120

Г) 115

Сколько пятизначных чисел можно составить из цифр 1,2,3,4,5 так, чтобы 3 и 4 были рядом?

А) 120

Б) 6

В) 117

Г) 48

Научное общество состоит из 25 человек. Надо выбрать президента общества, вице-президента, ученого секретаря и казначея. Сколькими способами может быть сделан этот выбор, если каждый член общества должен занимать только один пост?

А) 303600

Б) 25!

В) 506

Г) 6375600

А) (n-4)(n-5)

Б) (n-2)(n-1)n

В)

Г)

А) -2

Б) -3

В) 2

Г) 5

Сколькими способами можно расположить на шахматной доске 8 ладей так, чтобы они не могли бить друг друга?

А) 70

Б) 1680

В) 64

Г)40320

А)

Б) (2 m-1)

В) 2m

Г) (2 m-2)!

А) (n-5)!

Б)

В)

Г) n(n-1)(n-2)

А) 6

Б) 4

В) 5

Г) 3

А) -1

Б) 6

В) 27

Г)-22

А) 1

Б) 0

В) 3

Г) 4

А) 9

Б) 0.5

В) 1.5

Г) 0.3

Сочетание вычисляется по формуле

А) !

Б)

B) P(A)=

Г)

Размещения вычисляются по формуле

А) P(A)=

Б)

B)

Г) !

Перестановки из n элементов –это

А) выбор элементов из множества « n »

Б) количество элементов в множестве « n »

В) подмножество множества из n элементов

Г) установленный порядок во множестве « n »

Размещения применяются в задаче, если

А) происходит выбор элементов из множества с учетом порядка

Б) происходит выбор элементов из множества без учета порядка

В) необходимо осуществлять перестановку во множестве

Г) если все отобранные элементы одинаковы

В урне 6 белых и 5 черных шаров. Сколькими способами можно вынуть из нее 2 белых и 3 черных шара?

А)

Б)

В)

Г)

Среди 100 лотерейных билетов 45 выигрышных. Сколькими способами можно из трех купленных билетов получить выигрыш на одном?

А) 45

Б)

В)

Г)

Ответы к тесту №1

Ответы к тесту №2

Тест№2

«Основы теории вероятностей»

Случайным событием называется

А) такой исход эксперимента, при котором ожидаемый результат может произойти, а может не произойти

Б) такой исход эксперимента, который уже известен заранее

В) такой исход эксперимента, который нельзя определить заранее

Г) такой исход эксперимента, который при сохранении условий эксперимента постоянно повторяется

Союз «и» означает

А) сложение вероятностей событий

Б) умножение вероятностей событий

Г) деление вероятностей событий

Союз «или» означает

А) деление вероятностей событий

Б) сложение вероятностей событий

В) разность вероятностей событий

Г) умножение вероятностей событий

События, при которых наступление одного из них исключает наступление другого, называются

А) несовместными

Б) независимыми

В) зависимыми

Г) совместными

Полную группу событий образует

А) совокупность независимых событий, если в результате единичных испытаний произойдет обязательно одно из этих событий

Б) совокупность независимых событий, если в результате единичных испытаний произойдут обязательно все эти события

В) совокупность несовместных событий, если в результате единичных испытаний произойдет обязательно одно из этих событий

Г) совокупность несовместных событий, если в результате единичных испытаний произойдут обязательно все эти события

Противоположными называются

А) два независимых, образующих полную группу, событий

Б) два независимых события

В) два несовместных события

Г) два несовместных, образующих полную группу, событий

Независимыми называются два события

А) которые в результате испытания обязательно произойдут

Б) которые в результате испытания никогда не происходят вместе

В) в которых исход одного из них не зависит от исхода другого события

Г) в которых исход одного из них полностью зависит от исхода другого события

Событие, которое в результате испытания обязательно произойдет

А) невозможное

Б) точное

В) достоверное

Г) случайное

Событие, которое в результате испытания никогда не произойдет

А) невозможное

Б) точное

В) достоверное

Г) случайное

Наибольшее значение вероятности равно

А) 100%

Б) 1

В) бесконечность

Г) 0

Сумма вероятностей противоположных событий равна

А) 0

Б) 100%

В) -1

Г) 1

Фраза «хотя бы один» означает

А) только один элемент

Б) ни одного элемента

Г) один, два и не больше элементов

Классическое определение вероятности

А) вероятностью события называется отношение числа исходов, благоприятствующих наступлению события, к числу всех несовместных, единственно возможных и равновозможных исходов, образующих полную группу событий.

Б) Вероятность есть мера возможности наступления события в том или ином испытании

В) Вероятностью называется отношение числа испытаний, при которых событие произошло, к числу всех испытаний, при проведении которых событие могло произойти или не произойти.

Г) Каждому случайному событию А из поля событий ставится в соответствие неотрицательное число Р(А), называемое вероятностью.

Вероятность есть мера возможности наступления события в том или ином испытании

Это определение вероятности

А) классическое

Б) геометрическое

В) аксиоматическое

Г) статистическое

Вероятностью называется отношение числа испытаний, при которых событие произошло, к числу всех испытаний, при проведении которых событие могло произойти или не произойти. Это определение вероятности

А) классическое

Б) геометрическое

В) аксиоматическое

Г) статистическое

Условная вероятность вычисляется по формуле

А) Р(А/В)=

Б) Р(А+В)=Р(А)+Р(В)-Р(АВ)

В) Р(АВ)=Р(А)Р(В)

Г) Р(А+В)=Р(А)+Р(В)

Эта формула Р(А+В)=Р(А)+Р(В)-Р(АВ)применяется для двух

А) несовместных событий

Б) совместных событий

В) зависимых событий

Г) независимых событий

Для каких двух событий применяется понятие условной вероятности

А) невозможных

Б) достоверных

В) совместных

Г) зависимых

Формула полной вероятности

А) Р(H I /A)=

Б) Р(А)=Р(А/ H 1 ) P (H 1 )+ Р(А/ H 2 ) P (H 2 )+…+ Р(А/ H n ) P (H n )

В) P n (m )=

Г) Р(А)=

Б) теорема Байеса

В) схема Бернулли

А) формула полной вероятности

Б) теорема Байеса

В) схема Бернулли

Г) классическое определение вероятности

Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 6

А) Р(А)=

Б) Р(А)=

В) Р(А)=

Г) Р(А)=

Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков 11, а разность 5

А) Р(А)=0

Б) Р(А)=2/36

В) Р(А)= 1

Г) Р(А)=1/6

Прибор, работающий в течение суток, состоит из трех узлов, каждый из которых независимо от других, может за это время выйти из строя. Неисправность любого из узлов выводит из строя весь прибор. Вероятность исправной работы в течение суток первого узла равна 0,9, второго-0,85, третьего-0,95. С какой вероятностью прибор будет работать в течение суток безотказно?

А) Р(А)=0,1·0,15·0,05=0,00075

Б) Р(А)=0,9·0,85·0,95=0,727

В) Р(А)=0,1+0,85·0,95=0,91

Г) Р(А)=0,1·0,15·0,95=0,014

Задумано двузначное число, цифры которого различны. Найти вероятность того, что окажется равным задуманному числу случайно названное двузначное число?

А) Р(А)=0,1

Б) Р(А)=2/90

В) Р(А)= 1/100

Г) Р(А)=0,9

Двое стреляют по мишени с одинаковой вероятностью попадания равной 0,8. Какова вероятность поражения мишени?

А) Р(А)=0,8·0,8=0,64

Б) Р(А)=1-0,2·0,2=0,96

В) Р(А)=0,8·0,2+0,2·0,2=0,2

Г) Р(А)=1-0,8=0,2

Два ученика ищут нужную им книгу. Вероятность того, что книгу найдет первый ученик, равна 0,6, а второй 0,7. Какова вероятность того, что только один из учеников найдет нужную книгу?

А) Р(А)=1-0,6·0,7=0,58

Б) Р(А)=1-0,4·0,3=0,88

В) Р(А)=0,6·0,3+0,7·0,4=0,46

Г) Р(А)=0,6·0,7+0,3·0,4=0,54

Из колоды в 32 карты взяты наудачу одна за другой две карты. Найти вероятность того, что взяты два короля?

А) Р(А)=0,012

Б) Р(А)= 0,125

В) Р(А)=0,0625

Г) Р(А)=0,031

Три стрелка независимо друг от друга стреляют по мишени. Вероятность попадания в цель для первого стрелка равна 0,75, для второго 0,8, для третьего 0,9. Найти вероятность того, что в цель попадет хотя бы один стрелок?

А) Р(А)= 0,25·0,2·0,1=0,005

Б) Р(А)=0,75·0,8·0,9=0.54

В) Р(А)=1-0,25·0,2·0,1=0,995

Г) Р(А)=1-0,75·0,8·0,9=0,46

В ящике 10 одинаковых деталей, помеченных номерами от №1 до №10. Наудачу берут 6 деталей. Найти вероятность того, что среди извлеченных деталей будет деталь №5?

А) Р(А)= 5/10=0,2

Б) Р(А)=

В) Р(А)= 1/10=0,1

Г) Р(А)=

Найти вероятность того, что среди взятых наудачу 4 изделий 3 будет с браком, если в партии из 100 изделий 10-бракованных.

А) Р(А)=

Б) Р(А)=

В) Р(А)=

Г) Р(А)=

В вазе 10 белых и 8 алых роз. Наудачу берут два цветка. Какова вероятность того. Что они разного цвета?

А) Р(А)=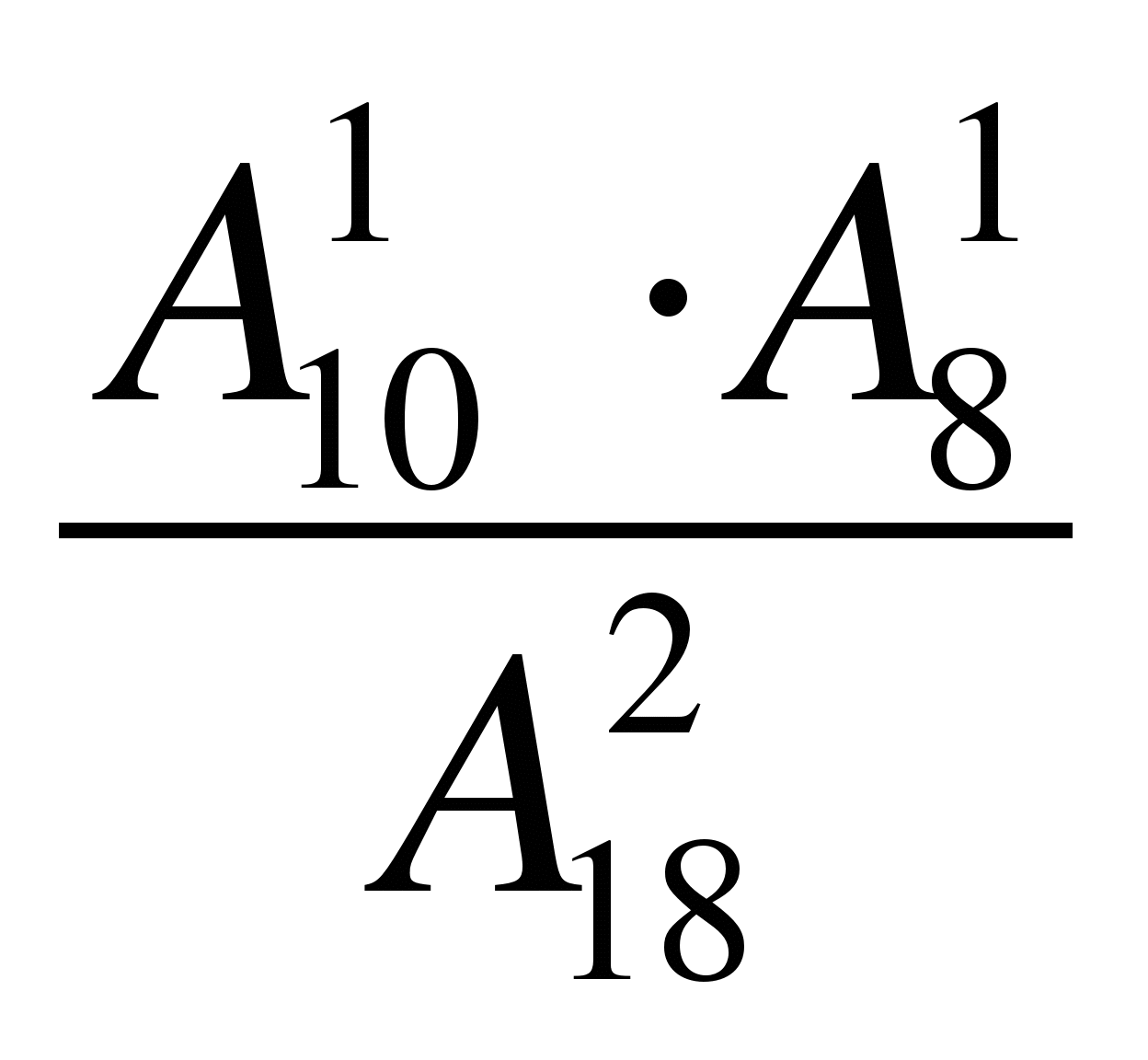

Б) Р(А)=

В) Р(А)=

Г) Р(А)= 2/18

Вероятность попадания в мишень при одном выстреле равна 1/8. Какова вероятность того, что из 12 выстрелов не будет ни одного промаха?

А) Р 12 (12)=

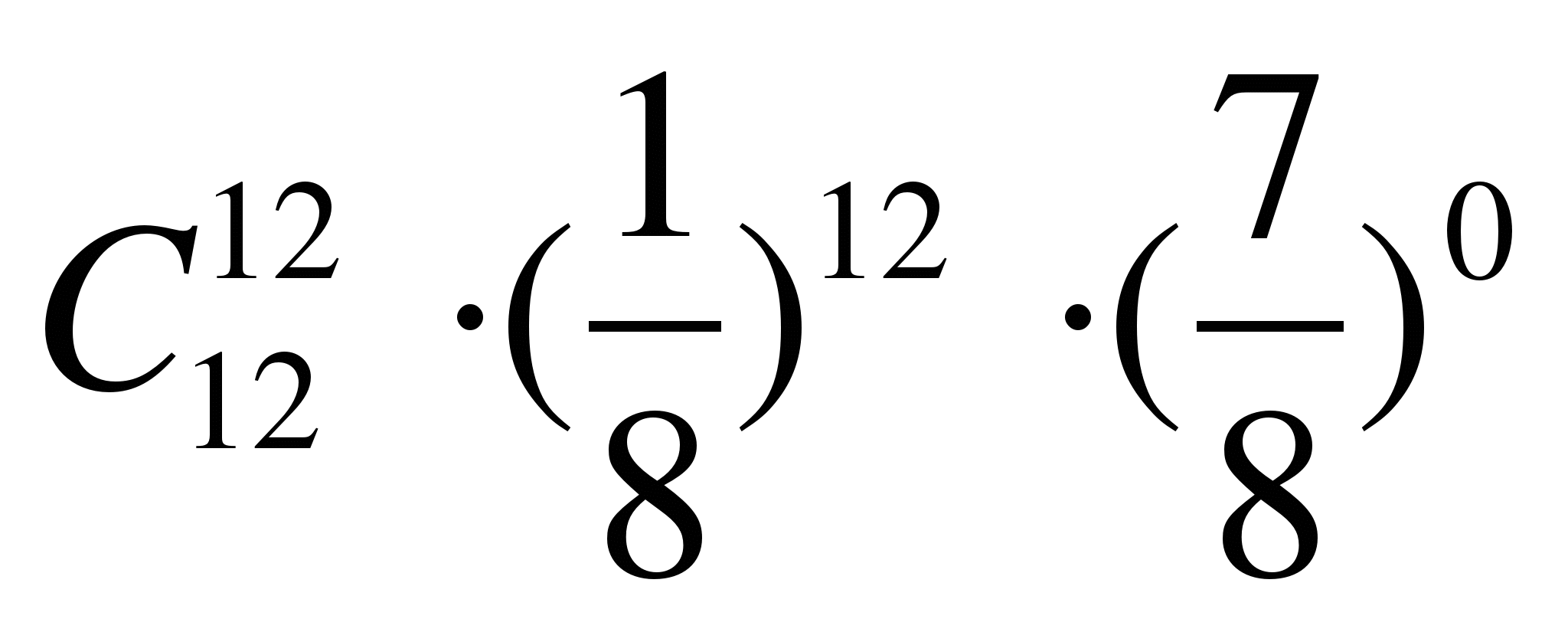
Б) Р 12 (1)=

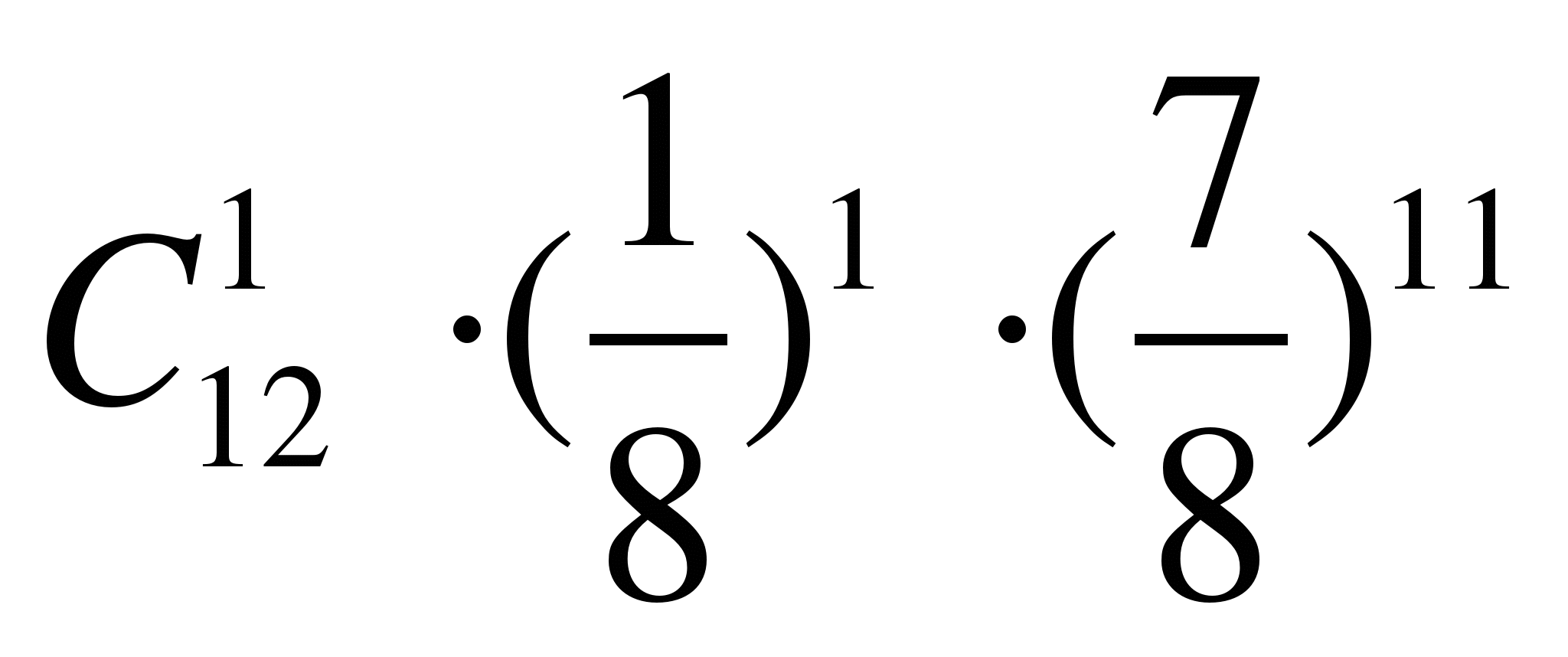
В) Р(А)=

Г) Р(А)=

Вратарь парирует в среднем 30% всех одиннадцатиметровых штрафных ударов. Какова вероятность того, что он возьмет 2 из 4 мячей?

А) Р 4 (2)=

Б) Р 4 (2)=

В) Р 4 (2)=

Г) Р 4 (2)=

В питомнике 40 вакцинированных кроликов и 10 контрольных. Осуществляют проверку подряд 14 кроликов, результат регистрируют и отправляют кроликов обратно. Определить наивероятнейшее число появления контрольного кролика.

А) 10

Б) 14

В) 14

Г) 14

Изделия высшего сорта на обувной фабрике составляют 10% всей продукции. Сколько пар сапог высшего сорта можно надеяться найти среди 75 пар, поступивших с этой фабрики в магазин?

А)75

Б) 75

В) 75

Г) 75

А) Локальная формула Лапласа

Б) Интегральная формула Лапласа

В)формула Муавра- Лапласа

Г) Схема Бернулли

При решении задачи «Вероятность появления брака в серии деталей равна 2%. Какова вероятность того, что в партии из 600 деталей окажется 20 бракованных?» более применима

А) схема Бернулли

Б) формула Муавра – Лапласа

В) локальная формула Лапласа

При решении задачи «В каждом из 700 независимых испытаний на брак, появление стандартной лампочки происходит с постоянной вероятностью 0,65. Найти вероятность того, что при таких условиях, появление бракованной лампочки произойдет чаще, чем в 230 испытаниях, но реже, чем в 270 случаях» более применима

А) схема Бернулли

Б) формула Муавра – Лапласа

В) локальная формула Лапласа

Г) интегральная формула Лапласа

Набирая номер телефона, абонент забыл цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра?

А) Р(А)=1/9

Б) Р(А)=1/10

В) Р(А)=1/99

Г) Р(А)=1/100

Брошена игральная кость. Найти вероятность того, что выпадет четное число очков?

А) Р(А)= 5/6

Б) Р(А)=1/6

В) Р(А)=3/6

Г) Р(А)=1

В ящике имеется 50 одинаковых деталей, из них 5 окрашенных. Наудачу вынимают одну деталь. Найти вероятность того, что извлеченная деталь окажется окрашенной?

А) Р(А)=0,1

Б) Р(А)=

В) Р(А)=

Г) Р(А)=0,3

В урне 3 белых и 9 черных шаров. Из урны одновременно вынимают 2 шара. Какова вероятность того, что оба шара белые?

А) Р(А)=

Б) Р(А)=

В) Р(А)=2/12

Г) Р(А)=

10 различных книг расставляются наудачу на одной полке. Найти вероятность того, что 3 определенные книги окажутся поставленные рядом?

А) Р(А)=

Б) Р(А)=

В)Р(А)=

Г) Р(А)=

Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5?

А) Р(А)=5/100

Б) Р(А)=1/100

В) Р(А)=

Г) Р(А)=

Тест №3

«Дискретные случайные величины»

Величина, которая в зависимости от результата эксперимента, может принимать различные числовые значения, называется

А) случайной

Б) дискретной

В) непрерывной

Г) вероятностью

Дискретной случайной величиной называется

А) величина, которая в зависимости от результата эксперимента, может принимать различные числовые значения

Б) величина, которая изменяется от одного испытания к другому с определенной вероятностью

В) величина, которая не изменяется при нескольких испытаниях

Г) величина, которая не зависимо от результата эксперимента, может принимать различные числовые значения

Модой называется

А) среднее значение дискретной случайной величины

Б) сумма произведений значений случайной величины на их вероятность

В) математическое ожидание квадрата отклонения величины от ее математического ожидания

Г) значение дискретной случайной величины, вероятность которого наибольшая

Среднее значение дискретной случайной величины называется

А) модой

Б) математическим ожиданием

В) медианой

Сумма произведений значений случайной величины на их вероятность называется

А) дисперсией

Б) математическим ожиданием

В) модой

Г) средним квадратичным отклонением

Математическое ожидание квадрата отклонения величины от ее математического ожидания

А) мода

Б) медиана

В) среднее квадратичное отклонение

Г) дисперсия

Формула, по которой вычисляется дисперсия

А)

Б) М(х 2 )-М(х)

В) М(х 2 )-(М(х)) 2

Г) (М(х)) 2 -М(х 2 )

Формула, по которой вычисляется математическое ожидание

А)

Б) М(х 2 )-(М(х)) 2

В)

Г)

По заданному ряду распределения дискретной случайной величины найти математическое ожидание

А) 1

Б) 1,3

В) 0,5

Г) 0,8

По заданному ряду распределения дискретной случайной величины найти М(х 2 )

А) 1,5

Б) 2,25

В) 2,9

Г) 0,99

Найти неизвестную вероятность

А) 0,65

Б) 0,75

В) 0

Г) 1

Найти моду

А) 0,03

Б) 1,7

В) 0,28

Г) 1,2

Найти медиану

А) 0,08

Б) 1,2

В) 4

Г) 0,28

Найти медиану

А) 1,2

Б) 3,5

В) 0,25

Г) 1,1

Найти неизвестное значение х, если М(х)=1,1

А) 3

Б) 1,1

В) 1,2

Г) 0

Математическое ожидание постоянной величины равно