We figured out how to find the area of ​​a curvilinear trapezoid G. Here are the resulting formulas:
for a continuous and non-negative function y=f(x) on the segment ,
for a continuous and non-positive function y=f(x) on the segment .

However, when solving problems of finding the area, one often has to deal with more complex figures.

In this article, we will talk about calculating the area of ​​figures whose boundaries are explicitly specified by functions, that is, as y=f(x) or x=g(y) , and analyze in detail the solution of typical examples.

Page navigation.

Formula for calculating the area of ​​a figure bounded by lines y=f(x) or x=g(y) .

Theorem.

Let the functions and be defined and continuous on the segment , and for any value x from . Then area of ​​figure G, bounded by lines x=a , x=b , and is calculated by the formula .

A similar formula is valid for the area of ​​\u200b\u200bthe figure bounded by the lines y \u003d c, y \u003d d, and: .

Proof.

Let us show the validity of the formula for three cases:

In the first case, when both functions are non-negative, due to the additivity property of the area, the sum of the area of ​​the original figure G and the curvilinear trapezoid is equal to the area of ​​the figure. Consequently,

That's why, . The last transition is possible due to the third property of the definite integral.

Similarly, in the second case, the equality is true. Here is a graphic illustration:

In the third case, when both functions are nonpositive, we have . Let's illustrate this:

Now we can move on to the general case when the functions and cross the Ox axis.

Let's denote the intersection points. These points divide the segment into n parts , where . The figure G can be represented by the union of the figures . It is obvious that on its interval falls under one of the three cases considered earlier, therefore their areas are found as

Consequently,

The last transition is valid due to the fifth property of the definite integral.

Graphic illustration of the general case.

Thus the formula proven.

It's time to move on to solving examples for finding the area of ​​figures bounded by the lines y=f(x) and x=g(y) .

Examples of calculating the area of ​​a figure bounded by lines y=f(x) or x=g(y) .

We will begin the solution of each problem by constructing a figure on a plane. This will allow us to represent a complex figure as a union of simpler figures. In case of difficulties with the construction, refer to the articles:; and .

Example.

Calculate the area of ​​a figure bounded by a parabola and straight lines , x=1 , x=4 .

Solution.

Let's build these lines on the plane.

Everywhere on the segment, the graph of a parabola above straight. Therefore, we apply the previously obtained formula for the area and calculate the definite integral using the Newton-Leibniz formula:

Let's complicate the example a bit.

Example.

Calculate the area of ​​the figure bounded by lines.

Solution.

How is this different from previous examples? Previously, we always had two straight lines parallel to the x-axis, and now only one x=7 . The question immediately arises: where to take the second limit of integration? Let's take a look at the drawing for this.

It became clear that the lower limit of integration when finding the area of ​​\u200b\u200bthe figure is the abscissa of the point of intersection of the graph of the straight line y \u003d x and the semi-parabola. We find this abscissa from the equality:

Therefore, the abscissa of the intersection point is x=2 .

Note.

In our example and in the drawing, it can be seen that the lines and y=x intersect at the point (2;2) and the previous calculations seem redundant. But in other cases, things may not be so obvious. Therefore, we recommend that you always analytically calculate the abscissas and ordinates of the points of intersection of lines.

Obviously, the graph of the function y=x is located above the graph of the function on the interval . We apply the formula to calculate the area:

Let's complicate the task even more.

Example.

Calculate the area of ​​the figure bounded by the graphs of functions and .

Solution.

Let's build a graph of inverse proportionality and a parabola .

Before applying the formula for finding the area of ​​a figure, we need to decide on the limits of integration. To do this, we find the abscissas of the intersection points of the lines by equating the expressions and .

For values ​​of x other than zero, the equality equivalent to third degree equation with integer coefficients. You can refer to the section to recall the algorithm for solving it.

It is easy to check that x=1 is the root of this equation: .

Dividing the expression to the binomial x-1 , we have:

Thus, the remaining roots are found from the equation :

Now from the drawing it became clear that the figure G is enclosed above the blue and below the red line in the interval . Thus, the required area will be equal to

Let's look at another typical example.

Example.

Calculate the area of ​​a figure bounded by curves and the abscissa axis.

Solution.

Let's make a drawing.

This is an ordinary power function with an exponent of one third, the plot of the function can be obtained from the graph by displaying it symmetrically about the x-axis and lifting it up by one.

Find the intersection points of all lines.

The x-axis has the equation y=0 .

The graphs of the functions and y=0 intersect at the point (0;0) since x=0 is the only real root of the equation.

Function Graphs and y=0 intersect at (2;0) , since x=2 is the only root of the equation .

Function graphs and intersect at the point (1;1) since x=1 is the only root of the equation . This statement is not entirely obvious, but is a strictly increasing function, and - strictly decreasing, therefore, the equation has at most one root.

The only remark: in this case, to find the area, you will have to use a formula of the form . That is, the bounding lines must be represented as functions of the argument y , but with a black line .

Let's define the points of intersection of the lines.

Let's start with graphs of functions and :

Let's find the point of intersection of graphs of functions and :

It remains to find the point of intersection of the lines and :

As you can see, the values ​​match.

Summarize.

We have analyzed all the most common cases of finding the area of ​​a figure bounded by explicitly given lines. To do this, you need to be able to build lines on a plane, find the points of intersection of lines and apply the formula to find the area, which implies the ability to calculate certain integrals.

Calculate the area of ​​a figure bounded by lines.

Solution.

We find the points of intersection of the given lines. To do this, we solve the system of equations:

To find the abscissas of the points of intersection of the given lines, we solve the equation:

We find: x 1 = -2, x 2 = 4.

So, these lines, which are a parabola and a straight line, intersect at points A(-2; 0), B(4; 6).

These lines form a closed figure, the area of ​​\u200b\u200bwhich is calculated using the above formula:

According to the Newton-Leibniz formula, we find:

Find the area of ​​an area bounded by an ellipse.

Solution.

From the ellipse equation for the I quadrant we have . From here, according to the formula, we obtain

Let's apply the substitution x = a sin t, dx = a cos t dt. New limits of integration t = α and t = β are determined from the equations 0 = a sin t, a = a sin t. Can be put α = 0 and β = π /2.

We find one fourth of the required area

From here S = pab.

Find the area of ​​a figure bounded by linesy = - x 2 + x + 4 andy = - x + 1.

Solution.

Find the intersection points of the lines y = -x 2 + x + 4, y = -x+ 1, equating the ordinates of the lines: - x 2 + x + 4 = -x+ 1 or x 2 - 2x- 3 = 0. Find the roots x 1 = -1, x 2 = 3 and their corresponding ordinates y 1 = 2, y 2 = -2.

Using the figure area formula, we get

Find the area enclosed by the parabolay = x 2 + 1 and directx + y = 3.

Solution.

Solving the system of equations

find the abscissas of the intersection points x 1 = -2 and x 2 = 1.

Assuming y 2 = 3 - x and y 1 = x 2 + 1, based on the formula we get

Calculate the area contained within the Bernoulli lemniscater 2 = a 2 cos 2 φ .

Solution.

In the polar coordinate system, the area of ​​the figure bounded by the arc of the curve r = f(φ ) and two polar radii φ 1 = ʅ and φ 2 = ʆ , is expressed by the integral

Due to the symmetry of the curve, we first determine one-fourth of the desired area

Therefore, the total area is S = a 2 .

Calculate the arc length of an astroidx 2/3 + y 2/3 = a 2/3 .

Solution.

We write the equation of the astroid in the form

(x 1/3) 2 + (y 1/3) 2 = (a 1/3) 2 .

Let's put x 1/3 = a 1/3 cos t, y 1/3 = a 1/3 sin t.

From here we obtain the parametric equations of the astroid

x = a cos 3 t, y = a sin 3 t, (*)

where 0 ≤ t ≤ 2π .

In view of the symmetry of the curve (*), it suffices to find one fourth of the arc length L corresponding to the parameter change t from 0 to π /2.

We get

dx = -3a cos 2 t sin t dt, dy = 3a sin 2 t cos t dt.

From here we find

Integrating the resulting expression in the range from 0 to π /2, we get

From here L = 6a.

Find the area bounded by the spiral of Archimedesr = aφ and two radius vectors that correspond to polar anglesφ 1 andφ 2 (φ 1 < φ 2 ).

Solution.

Area bounded by a curve r = f(φ ) is calculated by the formula , where α and β - limits of change of the polar angle.

Thus, we get

(*)

From (*) it follows that the area bounded by the polar axis and the first turn of the Archimedes spiral ( φ 1 = 0; φ 2 = 2π ):

Similarly, we find the area bounded by the polar axis and the second turn of the Archimedes spiral ( φ 1 = 2π ; φ 2 = 4π ):

The required area is equal to the difference of these areas

Calculate the volume of a body obtained by rotation around an axisOx figure bounded by parabolasy = x 2 andx = y 2 .

Solution.

Let's solve the system of equations

and get x 1 = 0, x 2 = 1, y 1 = 0, y 2 = 1, whence the intersection points of the curves O(0; 0), B(eleven). As can be seen in the figure, the desired volume of the body of revolution is equal to the difference between the two volumes formed by rotation around the axis Ox curvilinear trapezoids OCBA and ODBA:

Calculate the area bounded by the axisOx and sinusoidy = sinx on segments: a); b) .

Solution.

a) On the segment, the function sin x preserves the sign, and therefore by the formula , assuming y= sin x, we find

b) On the segment , function sin x changes sign. For the correct solution of the problem, it is necessary to divide the segment into two and [ π , 2π ], in each of which the function retains its sign.

According to the rule of signs, on the segment [ π , 2π ] area is taken with a minus sign.

As a result, the desired area is equal to

Determine the volume of the body bounded by the surface obtained from the rotation of the ellipsearound the major axisa .

Solution.

Given that the ellipse is symmetrical about the coordinate axes, it is enough to find the volume formed by rotation around the axis Ox area OAB, equal to one quarter of the area of ​​the ellipse, and double the result.

Let us denote the volume of the body of revolution through V x; then, based on the formula, we have , where 0 and a- abscissas of points B and A. From the equation of the ellipse we find . From here

Thus, the required volume is equal to . (When the ellipse rotates around the minor axis b, the volume of the body is )

Find the area bounded by parabolasy 2 = 2 px andx 2 = 2 py .

Solution.

First, we find the coordinates of the intersection points of the parabolas in order to determine the integration interval. Transforming the original equations, we obtain and . Equating these values, we get or x 4 - 8p 3 x = 0.

x 4 - 8p 3 x = x(x 3 - 8p 3) = x(x - 2p)(x 2 + 2px + 4p 2) = 0.

We find the roots of the equations:

Considering the fact that the point A the intersection of the parabolas is in the first quarter, then the limits of integration x= 0 and x = 2p.

The desired area is found by the formula

In this lesson we will learn how to calculate areas of flat figures, which are called curvilinear trapezoids .

Examples of such figures are in the figure below.

On the one hand, finding the area of ​​a flat figure using a definite integral is extremely simple. We are talking about the area of ​​\u200b\u200bthe figure, which is limited from above by a certain curve, from below - by the abscissa axis ( Ox), and on the left and right are some straight lines. The simplicity is that the definite integral of the function to which the curve is given, and there is the area of ​​such a figure(curvilinear trapezoid).

To calculate the area of ​​a figure, we need:

1. Definite integral of the function defining the curve , which limits the curvilinear trapezoid from above. And here comes the first significant nuance: a curvilinear trapezoid can be limited by a curve not only from above, but also from below . How to act in this case? Simple but important to remember: the integral in this case is taken with a minus sign .
2. Limits of integration a and b, which we find from the equations of lines that bound the figure on the left and right: x = a , x = b, where a and b- numbers.

Separately, some more nuances.

The curve that limits the curvilinear trapezoid from above (or below) must be graph of a continuous and non-negative function y = f(x) .

X values ​​must belong to the segment [a, b] . That is, such, for example, lines as a section of a mushroom are not taken into account, in which the leg fits perfectly into this segment, and the hat is much wider.

Side segments can degenerate into points . If you saw such a figure in the drawing, this should not confuse you, since this point always has its own value on the x-axis. So everything is in order with the limits of integration.

Now you can move on to formulas and calculations. So the area s curvilinear trapezoid can be calculated by the formula

If f(x) ≤ 0 (the graph of the function is located below the axis Ox), then area of ​​a curved trapezoid can be calculated by the formula

There are also cases when both the upper and lower boundaries of the figure are functions, respectively y = f(x) and y = φ (x) , then the area of ​​such a figure is calculated by the formula

. (3)

We solve problems together

Let's start with cases where the area of ​​a figure can be calculated using formula (1).

Example 1Ox) and direct x = 1 , x = 3 .

Solution. Because y = 1/x> 0 on the segment , then the area of ​​the curvilinear trapezoid is found by the formula (1):

.

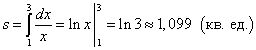Example 2 Find the area of ​​the figure bounded by the graph of the function , straight line x= 1 and the x-axis ( Ox ).

Solution. The result of applying formula (1):

If then s= 1/2; if then s= 1/3 , etc.

Example 3 Find the area of ​​\u200b\u200bthe figure bounded by the graph of the function, the x-axis ( Ox) and direct x = 4 .

Solution. The figure corresponding to the condition of the problem is a curvilinear trapezoid, in which the left segment has degenerated into a point. The integration limits are 0 and 4. Since, according to formula (1), we find the area of ​​the curvilinear trapezoid:

.

Example 4 Find the area of ​​the figure bounded by the lines , , and located in the 1st quarter.

Solution. To use formula (1), we represent the area of ​​the figure given by the conditions of the example as the sum of the areas of a triangle OAB and curvilinear trapezoid ABC. When calculating the area of ​​a triangle OAB the limits of integration are the abscissas of the points O and A, and for the figure ABC- abscissas of points A and C (A is the point of intersection of the line OA and parabolas, and C- point of intersection of the parabola with the axis Ox). Solving jointly (as a system) the equations of a straight line and a parabola, we obtain (the abscissa of the point A) and (the abscissa of another point of intersection of the line and the parabola, which is not needed for the solution). Similarly, we obtain , (abscissas of points C and D). Now we have everything to find the area of ​​the figure. We find:

Example 5 Find the area of ​​a curvilinear trapezoid ACDB, if the equation of the curve CD and abscissa A and B respectively 1 and 2.

Solution. We express this equation of the curve through Y: The area of ​​the curvilinear trapezoid is found by the formula (1):

.

Let's move on to cases where the area of ​​a figure can be calculated using formula (2).

Example 6 Find the area of ​​the figure bounded by the parabola and the x-axis ( Ox ).

Solution. This figure is located below the x-axis. Therefore, to calculate its area, we use formula (2). The limits of integration are the abscissas and points of intersection of the parabola with the axis Ox. Consequently,

Example 7 Find the area between the x-axis ( Ox) and two neighboring sine waves.

Solution. The area of ​​this figure can be found by the formula (2):

.

Let's find each term separately:

.

.

Finally we find the area:

.

Example 8 Find the area of ​​the figure enclosed between the parabola and the curve.

Solution. Let's express the equations of the lines in terms of Y:

The area according to the formula (2) will be obtained as

,

where a and b- abscissas of points A and B. We find them by solving the equations together:

Finally we find the area:

And, finally, there are cases when the area of ​​a figure can be calculated using formula (3).

Example 9 Find the area of ​​the figure enclosed between the parabolas and .

We now turn to the consideration of applications of the integral calculus. In this lesson, we will analyze a typical and most common task. calculating the area of ​​a flat figure using a definite integral. Finally, all those who seek meaning in higher mathematics - may they find it. You never know. In real life, you will have to approximate a summer cottage with elementary functions and find its area using a certain integral.

To successfully master the material, you must:

1) Understand the indefinite integral at least at an intermediate level. Thus, dummies should first read the lesson Not.

2) Be able to apply the Newton-Leibniz formula and calculate the definite integral. You can establish warm friendly relations with certain integrals on the page Definite integral. Solution examples. The task "calculate the area using a definite integral" always involves the construction of a drawing, therefore, your knowledge and drawing skills will also be an urgent issue. At a minimum, one must be able to build a straight line, a parabola and a hyperbola.

Let's start with a curvilinear trapezoid. A curvilinear trapezoid is a flat figure bounded by the graph of some function y = f(x), axis OX and lines x = a; x = b.

The area of ​​a curvilinear trapezoid is numerically equal to a certain integral

Any definite integral (that exists) has a very good geometric meaning. On the lesson Definite integral. Solution examples we said that a definite integral is a number. And now it's time to state another useful fact. From the point of view of geometry, the definite integral is the AREA. That is, the definite integral (if it exists) geometrically corresponds to the area of ​​some figure. Consider the definite integral

Integrand

defines a curve on the plane (it can be drawn if desired), and the definite integral itself is numerically equal to the area of ​​the corresponding curvilinear trapezoid.

Example 1

, , , .

This is a typical task statement. The most important point of the decision is the construction of a drawing. Moreover, the drawing must be built RIGHT.

When building a blueprint, I recommend the following order: first it is better to construct all lines (if any) and only after- parabolas, hyperbolas, graphs of other functions. The point-by-point construction technique can be found in the reference material Graphs and properties of elementary functions. There you can also find material that is very useful in relation to our lesson - how to quickly build a parabola.

In this problem, the solution might look like this.

Let's make a drawing (note that the equation y= 0 specifies the axis OX):

We will not hatch the curvilinear trapezoid, it is obvious what area we are talking about here. The solution continues like this:

On the interval [-2; 1] function graph y = x 2 + 2 located over axisOX, that's why:

Answer: .

Who has difficulty calculating the definite integral and applying the Newton-Leibniz formula

,

refer to the lecture Definite integral. Solution examples. After the task is completed, it is always useful to look at the drawing and figure out if the answer is real. In this case, “by eye” we count the number of cells in the drawing - well, about 9 will be typed, it seems to be true. It is quite clear that if we had, say, the answer: 20 square units, then, obviously, a mistake was made somewhere - 20 cells obviously do not fit into the figure in question, at most a dozen. If the answer turned out to be negative, then the task was also solved incorrectly.

Example 2

Calculate the area of ​​a figure bounded by lines xy = 4, x = 2, x= 4 and axis OX.

This is a do-it-yourself example. Full solution and answer at the end of the lesson.

What to do if the curvilinear trapezoid is located under axleOX?

Example 3

Calculate the area of ​​a figure bounded by lines y = e-x, x= 1 and coordinate axes.

Solution: Let's make a drawing:

If a curvilinear trapezoid completely under the axle OX , then its area can be found by the formula:

In this case:

.

Attention! The two types of tasks should not be confused:

1) If you are asked to solve just a definite integral without any geometric meaning, then it can be negative.

2) If you are asked to find the area of ​​a figure using a definite integral, then the area is always positive! That is why the minus appears in the formula just considered.

In practice, most often the figure is located in both the upper and lower half-planes, and therefore, from the simplest school problems, we move on to more meaningful examples.

Example 4

Find the area of ​​a plane figure bounded by lines y = 2x – x 2 , y = -x.

Solution: First you need to make a drawing. When constructing a drawing in area problems, we are most interested in the intersection points of lines. Find the intersection points of the parabola y = 2x – x 2 and straight y = -x. This can be done in two ways. The first way is analytical. We solve the equation:

So the lower limit of integration a= 0, upper limit of integration b= 3. It is often more profitable and faster to construct lines point by point, while the limits of integration are found out as if “by themselves”. Nevertheless, the analytical method of finding the limits still sometimes has to be used if, for example, the graph is large enough, or the threaded construction did not reveal the limits of integration (they can be fractional or irrational). We return to our task: it is more rational to first construct a straight line and only then a parabola. Let's make a drawing:

We repeat that in pointwise construction, the limits of integration are most often found out “automatically”.

And now the working formula:

If on the interval [ a; b] some continuous function f(x) greater than or equal some continuous function g(x), then the area of ​​the corresponding figure can be found by the formula:

Here it is no longer necessary to think where the figure is located - above the axis or below the axis, but it matters which chart is ABOVE(relative to another graph), and which one is BELOW.

In the example under consideration, it is obvious that on the segment the parabola is located above the straight line, and therefore from 2 x – x 2 must be subtracted - x.

The completion of the solution might look like this:

The desired figure is limited by a parabola y = 2x – x 2 top and straight y = -x from below.

On segment 2 x – x 2 ≥ -x. According to the corresponding formula:

Answer: .

In fact, the school formula for the area of ​​a curvilinear trapezoid in the lower half-plane (see example No. 3) is a special case of the formula

.

Since the axis OX is given by the equation y= 0, and the graph of the function g(x) is located below the axis OX, then

.

And now a couple of examples for an independent decision

Example 5

Example 6

Find the area of ​​a figure bounded by lines

In the course of solving problems for calculating the area using a certain integral, a funny incident sometimes happens. The drawing was made correctly, the calculations were correct, but, due to inattention, ... found the area of ​​the wrong figure.

Example 7

Let's draw first:

The figure whose area we need to find is shaded in blue.(carefully look at the condition - how the figure is limited!). But in practice, due to inattention, they often decide that they need to find the area of ​​\u200b\u200bthe figure that is shaded in green!

This example is also useful in that in it the area of ​​\u200b\u200bthe figure is calculated using two definite integrals. Really:

1) On the segment [-1; 1] above axle OX the graph is straight y = x+1;

2) On the segment above the axis OX the graph of the hyperbola is located y = (2/x).

It is quite obvious that the areas can (and should) be added, therefore:

Answer:

Example 8

Calculate the area of ​​a figure bounded by lines

Let's present the equations in the "school" form

and do the line drawing:

It can be seen from the drawing that our upper limit is “good”: b = 1.

But what is the lower limit? It is clear that this is not an integer, but what?

May be, a=(-1/3)? But where is the guarantee that the drawing is made with perfect accuracy, it may well turn out that a=(-1/4). What if we didn't get the graph right at all?

In such cases, one has to spend additional time and refine the limits of integration analytically.

Find the intersection points of the graphs

To do this, we solve the equation:

.

Consequently, a=(-1/3).

The further solution is trivial. The main thing is not to get confused in substitutions and signs. The calculations here are not the easiest. On the segment

, ,

according to the corresponding formula:

Answer:

In conclusion of the lesson, we will consider two tasks more difficult.

Example 9

Calculate the area of ​​a figure bounded by lines

Solution: Draw this figure in the drawing.

To draw a drawing point by point, you need to know the appearance of the sinusoid. In general, it is useful to know the graphs of all elementary functions, as well as some values ​​of the sine. They can be found in the table of values trigonometric functions. In some cases (for example, in this case), it is allowed to construct a schematic drawing, on which graphs and integration limits must be displayed in principle correctly.

There are no problems with the integration limits here, they follow directly from the condition:

- "x" changes from zero to "pi". We make a further decision:

On the segment, the graph of the function y= sin 3 x located above the axis OX, that's why:

(1) You can see how sines and cosines are integrated in odd powers in the lesson Integrals of trigonometric functions. We pinch off one sine.

(2) We use the basic trigonometric identity in the form

(3) Let us change the variable t= cos x, then: located above the axis , so:

.

.

Note: note how the integral of the tangent in the cube is taken, here the consequence of the basic trigonometric identity is used

.

Enter the function for which you want to find the integral

The calculator provides a DETAILED solution of definite integrals.

This calculator solves the definite integral of the function f(x) with the given upper and lower limits.

Examples

With the use of degree
(square and cube) and fractions

(x^2 - 1)/(x^3 + 1)

Square root

Sqrt(x)/(x + 1)

cube root

Cbrt(x)/(3*x + 2)

Using sine and cosine

2*sin(x)*cos(x)

Arcsine

X*arcsin(x)

Arc cosine

x*arccos(x)

Application of the logarithm

X*log(x, 10)

natural logarithm

Exhibitor

Tg(x)*sin(x)

Cotangent

Ctg(x)*cos(x)

Irrational fractions

(sqrt(x) - 1)/sqrt(x^2 - x - 1)

Arctangent

X*arctg(x)

Arc tangent

X*arсctg(x)

Hyberbolic sine and cosine

2*sh(x)*ch(x)

Hyberbolic tangent and cotangent

ctgh(x)/tgh(x)

Hyberbolic arcsine and arccosine

X^2*arcsinh(x)*arccosh(x)

Hyberbolic arctangent and arccotangent

X^2*arctgh(x)*arctgh(x)

Rules for entering expressions and functions

Expressions can consist of functions (notations are given in alphabetical order): absolute(x) Absolute value x
(module x or |x|) arccos(x) Function - arc cosine of x arccosh(x) Arc cosine hyperbolic from x arcsin(x) Arcsine from x arcsinh(x) Arcsine hyperbolic from x arctg(x) Function - arc tangent from x arctgh(x) The arc tangent is hyperbolic from x e e a number that is approximately equal to 2.7 exp(x) Function - exponent from x(which is e^x) log(x) or log(x) Natural logarithm of x
(To obtain log7(x), you need to enter log(x)/log(7) (or, for example, for log10(x)=log(x)/log(10)) pi The number is "Pi", which is approximately equal to 3.14 sin(x) Function - Sine of x cos(x) Function - Cosine of x sinh(x) Function - Hyperbolic sine of x cash(x) Function - Hyperbolic cosine of x sqrt(x) The function is the square root of x sqr(x) or x^2 Function - Square x tg(x) Function - Tangent from x tgh(x) Function - Hyperbolic tangent of x cbrt(x) The function is the cube root of x

You can use the following operations in expressions: Real numbers enter in the form 7.5 , not 7,5 2*x- multiplication 3/x- division x^3- exponentiation x + 7- addition x - 6- subtraction
Other features: floor(x) Function - rounding x down (example floor(4.5)==4.0) ceiling(x) Function - rounding x up (example ceiling(4.5)==5.0) sign(x) Function - Sign x erf(x) Error function (or probability integral) laplace(x) Laplace function